定义
形如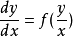 的一阶微分方程称为齐次微分方程,简称微分方程。
的一阶微分方程称为齐次微分方程,简称微分方程。
方程特点齐次微分方程的特点是其右端项是以 为变元的连续函数。
为变元的连续函数。
例如,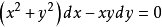 是齐次微分方程,它可以转化为:
是齐次微分方程,它可以转化为: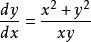 ,即
,即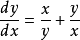 。1
。1
方程的解齐次微分方程通过变量代换,可化为可分离变量微分方程来求解。
令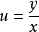 或
或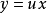 ,
,
其中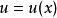 是新的未知函数,对
是新的未知函数,对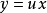 两边求导,则有:
两边求导,则有: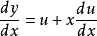 ,
,
将其代入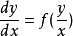 ,得:
,得: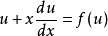 ,
,
分离变量,得: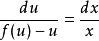
两边积分,得: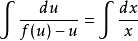 ,
,
求出积分后,再将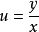 回代,便得到方程
回代,便得到方程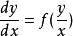 的通解。
的通解。
求解步骤(1)作变换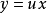 ,将齐次方程转化为分离变量的微分方程;
,将齐次方程转化为分离变量的微分方程;
(2)求解可分离变量的微分方程;
(3)用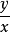 代替步骤(2)中所求通解中的
代替步骤(2)中所求通解中的 (即变量还原),就可以得到原方程的通解。1
(即变量还原),就可以得到原方程的通解。1
注意事项如果有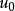 ,使得
,使得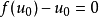 ,则显然
,则显然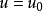 也是方程
也是方程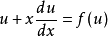 的解,从而
的解,从而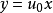 也是方程
也是方程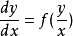 的解;如果
的解;如果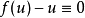 ,则方程
,则方程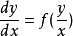 变成
变成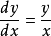 ,这是一个可分离变量微分方程。
,这是一个可分离变量微分方程。
典例例1求解方程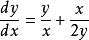 。
。
解:令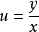 ,则
,则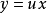 ,
,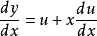 ,
,
原方程变为: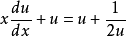 ,即
,即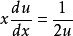 ;
;
分离变量可得: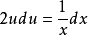 ,
,
左右两端同时积分可得: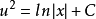 ,
,
将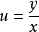 代入,便可得到原方程的通解为:
代入,便可得到原方程的通解为: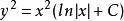 ,其中 C 为任意常数。1
,其中 C 为任意常数。1
例2求方程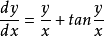 的通解。
的通解。
解:令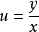 ,则
,则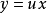 ,
,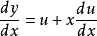 ,
,
原方程变为: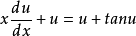 ,即
,即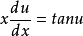 ;
;
分离变量可得: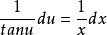 ,
,
左右两端同时积分可得: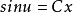 ,
,
将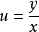 代入,便可得到原方程的通解为:
代入,便可得到原方程的通解为: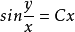 ,其中 C 为任意常数。2
,其中 C 为任意常数。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国