基本介绍
给定非空凸集C,我们说向量d是C的一个回收方向(direction ofrecession),如果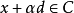 对所有的
对所有的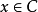 和
和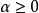 都成立。因此,d是C的一个回收方向,如果我们从C中任意的x点出发,沿着d的方向走到无穷,而永远都不穿过C的相对边界跑到C之外的点上去。
都成立。因此,d是C的一个回收方向,如果我们从C中任意的x点出发,沿着d的方向走到无穷,而永远都不穿过C的相对边界跑到C之外的点上去。
所有回收方向的集合是一个包含原点的锥体(core),我们称它为C的回收锥(recession cone),并记作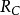 (参见图1)。于是,
(参见图1)。于是,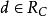 如果
如果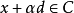 对所有的
对所有的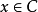 和
和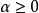 成立。闭凸集的一条重要性质就是为检验
成立。闭凸集的一条重要性质就是为检验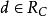 是否成立,只需要验证
是否成立,只需要验证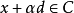 对单一的
对单一的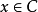 成立就可以了。这就是下述命题的(b)部分2。
成立就可以了。这就是下述命题的(b)部分2。
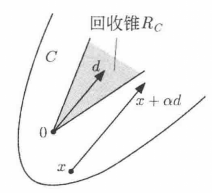
图1 凸集C的回收锥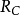 的图示。回收方向d满足
的图示。回收方向d满足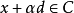 对所有
对所有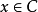 和
和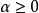 成立。
成立。
回收锥定理命题1(回收锥定理(Recession Cone Theorem))令C为非空闭凸集。
(a) 回收锥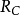 是闭的和凸的。
是闭的和凸的。
(b) 向量d属于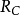 当且仅当存在向量
当且仅当存在向量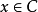 使得
使得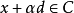 对所有
对所有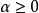 成立。
成立。
证明:(a) 如果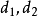 属于
属于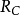 而
而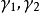 是正的标量使
是正的标量使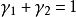 成立,我们有对任意的
成立,我们有对任意的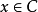 和
和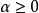
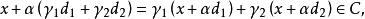 其中最后的包含关系成立是因为C是凸的,而根据
其中最后的包含关系成立是因为C是凸的,而根据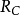 的定义
的定义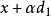 和
和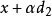 属于C。于是
属于C。于是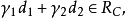 这表明
这表明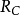 是凸的。
是凸的。
令d属于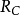 的闭包,并令
的闭包,并令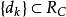 为收敛到d的点列。对于任意的
为收敛到d的点列。对于任意的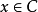 和
和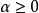 ,我们有
,我们有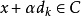 对所有k成立,并且因为C是闭的,
对所有k成立,并且因为C是闭的,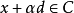 。于是
。于是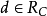 ,从而
,从而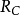 是闭的。
是闭的。
(b) 如果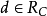 ,根据
,根据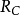 的定义,每个向量
的定义,每个向量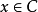 都具有所要求的性质。反之,令d使得存在向量
都具有所要求的性质。反之,令d使得存在向量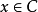 满足
满足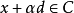 对所有
对所有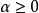 成立。不失一般性,假定d≠0。任取
成立。不失一般性,假定d≠0。任取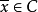 和
和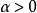 ,我们要证明
,我们要证明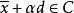 。事实上,只要证明
。事实上,只要证明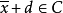 ,即假定
,即假定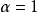 ,因为通过用
,因为通过用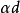 代替d可以把
代替d可以把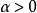 的一般情形可以归结为
的一般情形可以归结为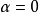 的情况。
的情况。
根据我们对x和d的选取,令
 可知
可知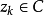 对所有k成立,如果
对所有k成立,如果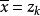 对某个k成立,那么
对某个k成立,那么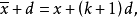 就属于C,而我们的证明完成。因此假设
就属于C,而我们的证明完成。因此假设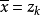 对所有k成立,并且定义
对所有k成立,并且定义
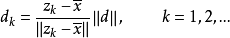 使得
使得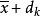 是以
是以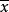 为球心以
为球心以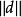 为半径的球面与从
为半径的球面与从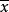 出发通过
出发通过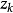 的射线的交点(参见图2中的构造方法),现在我们来论证,
的射线的交点(参见图2中的构造方法),现在我们来论证,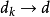 ,并且对于充分大的k,
,并且对于充分大的k,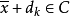 ,于是利用C的闭性,可导出
,于是利用C的闭性,可导出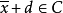 。
。
的确,据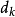 的定义,我们有
的定义,我们有
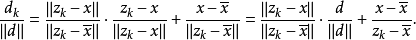 因为
因为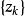 是无界点列,
是无界点列,

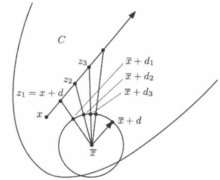
图2 命题1(b)的证明中用到的构造。
于是结合前面的关系,我们有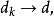 对所有满足
对所有满足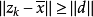 的k,在连接
的k,在连接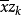 的线段上,向量
的线段上,向量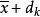 处在
处在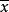 和
和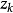 之间,因此由C的凸性,我们有
之间,因此由C的凸性,我们有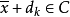 对所有充分大的k成立。因为
对所有充分大的k成立。因为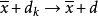 和C是闭的,可知
和C是闭的,可知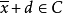 。
。
上述命题中集合C为闭的假设是实质性的。如果没有这个假设,(a)部分不成立的一个例子是,考虑集合
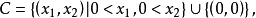 它的回收锥等于C,而它是非闭的。该例子中(b)部分也不成立,因为对于方向d=(1,0),我们有
它的回收锥等于C,而它是非闭的。该例子中(b)部分也不成立,因为对于方向d=(1,0),我们有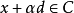 对所有
对所有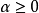 和除
和除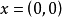 之外的所有
之外的所有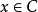 成立2。
成立2。
回收锥其他性质下述命题给出回收锥的一些其他性质。
**(回收锥的性质)**令C为非空闭凸集。
(a) 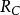 包含一个非零的方向当且仅当C是无界的。
包含一个非零的方向当且仅当C是无界的。
(b)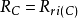 。
。
(c) 对任意一组闭凸集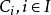 ,其中
,其中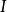 为任意指标集,并且
为任意指标集,并且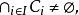 我们有
我们有
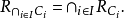
(d) 令W为m维欧氏空间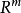 的一个紧的凸子集,并令A为m×n维矩阵,集合
的一个紧的凸子集,并令A为m×n维矩阵,集合
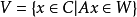 (假设该集合为非空) 的回收锥是
(假设该集合为非空) 的回收锥是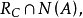 其中
其中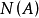 是A的化零空间(nullspace)2。
是A的化零空间(nullspace)2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国