回收方向(direction of recession)是指实线性空间的集合中的射线所定义的方向。设A为实线性空间X的集合,若h∈X且存在x∈A,使得对于任何λ≥0,有x+λh∈A,那么h称为A的回收方向1。
定义给定非空凸集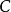 ,我们说向量
,我们说向量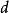 是
是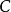 的一个回收方向(direction ofrecession),如果
的一个回收方向(direction ofrecession),如果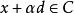 对所有的
对所有的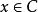 和
和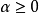 都成立。因此,
都成立。因此,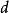 是
是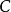 的一个回收方向,如果我们从
的一个回收方向,如果我们从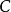 中任意的
中任意的 点出发,沿着
点出发,沿着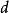 的方向走到无穷,而永远都不穿过
的方向走到无穷,而永远都不穿过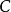 的相对边界跑到
的相对边界跑到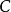 之外的点上去。
之外的点上去。
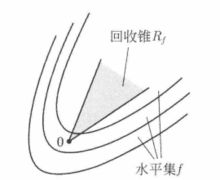
所有回收方向的集合是一个包含原点的锥体(core),我们称它为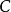 的回收锥(recession cone),并记作
的回收锥(recession cone),并记作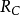 (参见图1)。于是,
(参见图1)。于是,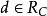 如果
如果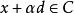 对所有的
对所有的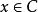 和
和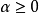 成立。闭凸集的一条重要性质就是为检验
成立。闭凸集的一条重要性质就是为检验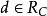 是否成立,只需要验证
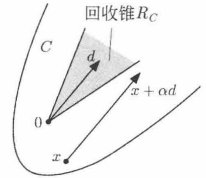
是否成立,只需要验证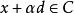 对单一的
对单一的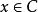 成立就可以了2。
成立就可以了2。
分析理解命题令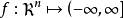 为闭的真凸函数,考虑水平集
为闭的真凸函数,考虑水平集
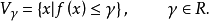 则:(a) 所有非空水平集
则:(a) 所有非空水平集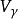 都具有相同的回收锥,记作
都具有相同的回收锥,记作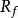 ,由
,由
 给出,其中
给出,其中 是
是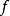 的上图的回收锥2。
的上图的回收锥2。
(b) 如果某个非空水平集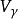 是紧的,那么所有这些水平集都是紧的。
是紧的,那么所有这些水平集都是紧的。
注意在命题(a) 中,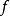 的闭性对于水平集
的闭性对于水平集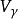 具有共同的回收锥是实质性的,读者可以用一个例子来验证这一点,考虑如下凸的但非闭的函数
具有共同的回收锥是实质性的,读者可以用一个例子来验证这一点,考虑如下凸的但非闭的函数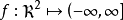 .它由
.它由
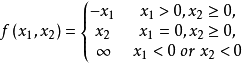 给出.这里,对
给出.这里,对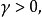 我们有
我们有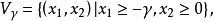 因此
因此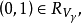 但
但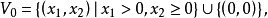 因此
因此
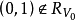 对于闭的真凸函数
对于闭的真凸函数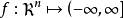 ,非空水平集的(公共) 回收锥
,非空水平集的(公共) 回收锥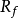 称为
称为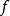 的回收锥(参见图2)。向量
的回收锥(参见图2)。向量 称为
称为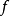 的回收方向。
的回收方向。
理解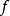 回收方向的最直观的方式是从一个下降的角度看问题:如果我们从任意
回收方向的最直观的方式是从一个下降的角度看问题:如果我们从任意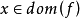 处出发,并且沿着回收方向随意运动,我们必然保持位于每个包含
处出发,并且沿着回收方向随意运动,我们必然保持位于每个包含 的水平集内,或者等价地,我们必然只遇到满足
的水平集内,或者等价地,我们必然只遇到满足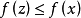 的点
的点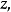 换句话说,
换句话说,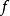 的回收方向就是对
的回收方向就是对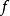 连续不上升的方向.反过来,如果我们从某个
连续不上升的方向.反过来,如果我们从某个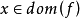 出发,而且在沿着方向d移动的时候,我们遇到点z满足
出发,而且在沿着方向d移动的时候,我们遇到点z满足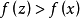 ,那么d不可能成为回收方向。由
,那么d不可能成为回收方向。由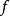 的水平集的凸性,一旦我们跨过水平集的相对边界,我们就永远不会再次跨越该边界,而且易知,一个方向若不是
的水平集的凸性,一旦我们跨过水平集的相对边界,我们就永远不会再次跨越该边界,而且易知,一个方向若不是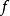 回收方向,将是
回收方向,将是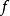 最终连续上升的方向[见图3(e),(f)]。
最终连续上升的方向[见图3(e),(f)]。
|| ||
闭的真凸函数在某个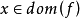 处沿着方向d的上升/下降行为,如果d是f的回收方向,就存在着两种可能性: 要么f单调减少到某个有限值或
处沿着方向d的上升/下降行为,如果d是f的回收方向,就存在着两种可能性: 要么f单调减少到某个有限值或 [分别对应图
[分别对应图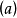 和
和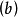 ],要么f达到小于等于
],要么f达到小于等于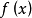 的某个值并且保持为该值[图
的某个值并且保持为该值[图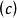 和
和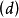 ],如果d不是f的回收方向,那么最终f会单调增加到
],如果d不是f的回收方向,那么最终f会单调增加到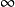 [图
[图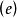 和
和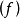 ],即对某个
],即对某个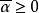 和所有满足
和所有满足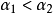 的
的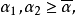 我们有
我们有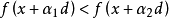 ,这样的行为仅决定于d,独立于x 在
,这样的行为仅决定于d,独立于x 在 中的选取2。
中的选取2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国