[科普中国]-赫弗里格定理

赫弗里格定理断言：如果M是一个紧的k连通流形，且n≥2k+3，则M可以被嵌入到R2n-k中。

简介赫弗里格定理是关于嵌入的一个定理。

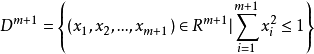该定理断言：如果M是一个紧的k连通流形，且n≥2k+3，则M可以被嵌入到R2n-k中，这里M称为k连通的，若对于任何m(0≤m≤k)，从球面到M的任何连续映射f，均可扩张为到M的连续映射F，即F:Dm+1→M连续，。1

嵌入嵌入是一对一的浸入，且流形与其像是同胚的映射。

设ψ:M→N是两个微分流形间的C∞映射，若ψ是一对一的浸入，且还是M与ψ(M)之间的同胚，则称ψ是一个嵌入。

流形流形是局部具有欧几里得空间性质的空间，在数学中用于描述几何形体。物理上，经典力学的相空间和构造广义相对论的时空模型的四维伪黎曼流形都是流形的实例。

n维流形M的边缘∂M是n-1维无边缘流形。紧的无边缘的连通流形称为闭流形，非紧的无边缘的连通流形称为开流形。存在连通的但非仿紧的拓扑流形。一维的这种流形称为长直线。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学