[科普中国]-傅里叶-斯蒂尔杰斯变换

傅里叶-斯蒂尔杰斯变换（Fourier-Stieltjes transform）是经典傅里叶-斯蒂尔杰斯变换的推广。

简介傅里叶-斯蒂尔杰斯变换是经典傅里叶-斯蒂尔杰斯变换的推广。

设G为局部紧交换群，Ĝ为G的对偶群，设M(G)为G上有界的正则复测度全体所成的集。对μ∈M(G)，定义Ĝ上的函数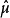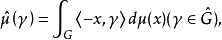：其中=γ(x)为G上的特征标，称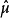为μ的傅里叶-斯蒂尔杰斯变换。

更一般地，有时也称映射μ→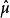为傅里叶-斯蒂尔杰斯变换。1

局部紧交换群(locally compact abelian group)

局部紧交换群是一类特殊的交换群。

设G是一个局部紧豪斯多夫空间，又是一个交换群，且映射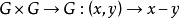是连续的，则称G为局部紧交换群，简称LCA群。

特征标特征标是一种特殊函数，即群G的与它的某个线性表示有密切关系的函数。

设ρ:G→GL(V)是群G的一个F线性表示。取定V的一个基，并假定在这一基下ρ对应的矩阵表示为T:G→GLn(F)。对g∈G，记tr(T(g))为矩阵T(g)的迹，即T(g)的主对角线元素之和。定义G上的F值函数𝜒(g)=tr(T(g))，g∈G，其取值与v的基选择无关，称这一函数为P所提供的F特征标。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所