[科普中国]-非阿基米德赋值

非阿基米德赋值（non-archimedian norm）是局部域上的一种特殊映射。

简介非阿基米德赋值是局部域上的一种特殊映射。

局部域K可以赋予非阿基米德范数|·|，使K成为一个赋值域。若对x,y∈K满足：

1、|x|=0⇔x=0；

2、|xy|=|x||y|；

3、|x+y|≤max(|x|,|y|)，则称映射x→|x|为K上的非阿基米德赋值（范数）。

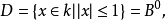
值域K上的非阿基米德范数的值域是数集{qk|k∈Z}∪{0}，其中q=pc，p为素数，c∈N。K的非0元β满足|β|=q-1。K的子集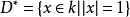分别称为K的分数理想、整环与K*的单位群。1

局部域在数学上，局部域是一类特别的域，它有非平凡的绝对值，此绝对值赋予的拓扑是局部紧的。

局部域可粗分为两类：一种的绝对值满足阿基米德性质（称作阿基米德局部域），另一种的绝对值不满足阿基米德性质（称作非阿基米德局部域）。在数论中，数域的完备化给出局部域的典型例子。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所