共轭傅里叶积分是一种特殊的积分变换。这个积分在很强的条件下才能是一个真正的收敛的积分。
简介共轭傅里叶积分是一种特殊的积分变换。
设 K 为满足方程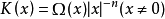 的核函数,
的核函数,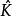 是 K 在广义函数意义下的傅里叶变换,设
是 K 在广义函数意义下的傅里叶变换,设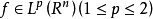 , f 的共轭傅里叶积分指的是形式积分
, f 的共轭傅里叶积分指的是形式积分
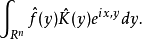 这个积分在很强的条件下才能是一个真正的收敛的积分。1
这个积分在很强的条件下才能是一个真正的收敛的积分。1
傅里叶乘子(Fouier multiplier)
傅里叶乘子通过傅里叶变换定义的一类算子。
设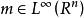 . 在
. 在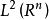 上定义算子Tm:Tm(f)=ℱ-1(m·
上定义算子Tm:Tm(f)=ℱ-1(m·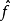 )(即ℱ (Tm(f))=m
)(即ℱ (Tm(f))=m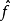 )。
)。
如果存在常数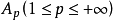 ,使得
,使得
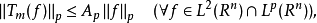 就称 m 为傅立叶 Lp 乘子,简称 Lp 乘子。由 m 所确定的算子 Tm称为乘子算子。若 m 是Lp乘子,则如上定义的算子 Tm 可保范延拓至整个 Lp(Rn),成为 Lp(Rn)到自身的有界线性算子。
就称 m 为傅立叶 Lp 乘子,简称 Lp 乘子。由 m 所确定的算子 Tm称为乘子算子。若 m 是Lp乘子,则如上定义的算子 Tm 可保范延拓至整个 Lp(Rn),成为 Lp(Rn)到自身的有界线性算子。
一般地,设 P,Q 是 Rn 上两个具有某种特性的函数类,m 是定义在 Rn 上的一个函数,Tm(f)=ℱ -1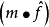 ,如对任一
,如对任一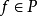 ,均有
,均有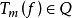 ,且
,且
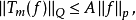 则称 Tm (或 m)为(P,Q)乘子。
则称 Tm (或 m)为(P,Q)乘子。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国