哈纳克不等式(Harnack inequality)是调和函数的重要性质,是指非负调和函数在圆周上的值与其在圆心的值之比的双向不等式,哈纳克不等式引出了一个强大而简单的定理,称为哈纳克原理。
定义设 是区域Ω中一个非负调和函数,则对Ω的任一紧子集Ω′,存在一个只依赖于n,Ω′和Ω的常数C,使得1
是区域Ω中一个非负调和函数,则对Ω的任一紧子集Ω′,存在一个只依赖于n,Ω′和Ω的常数C,使得1
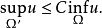 特别地,如果
特别地,如果 在以原点为中心,R为半径的球
在以原点为中心,R为半径的球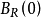 中是一个非负调和函数,那么哈纳克不等式有如下形式:
中是一个非负调和函数,那么哈纳克不等式有如下形式:
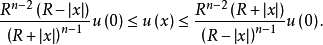
哈纳克原理泊松公式使我们可以将一个调和函数用它在一个圆周上的值来表示,为了适应目前的需要,我们把它写成形式
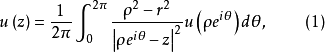 其中
其中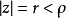 而
而 假定在
假定在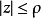 中调和(或对
中调和(或对 调和,对
调和,对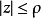 连续)。联系初等不等式
连续)。联系初等不等式
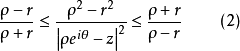 的右端,公式(1)给出估计
的右端,公式(1)给出估计
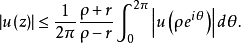 如果已知
如果已知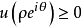 ,那么也可用(2)的第一个不等式,得到一个双重估计
,那么也可用(2)的第一个不等式,得到一个双重估计
 但
但 的算术平均等于
的算术平均等于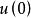 ,于是最后得到下面的上界与下界:
,于是最后得到下面的上界与下界:
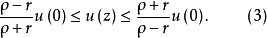 这是哈纳克不等式,我们要着重指出,它仅对正的调和函数为真。(3)的主要应用是用于正项级数,或等价地,用于调和函数的增序列。它引出一个强大而简单的定理,称为哈纳克原理2。
这是哈纳克不等式,我们要着重指出,它仅对正的调和函数为真。(3)的主要应用是用于正项级数,或等价地,用于调和函数的增序列。它引出一个强大而简单的定理,称为哈纳克原理2。
哈纳克原理:考察函数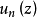 的一个序列,其中每个函数定义在某一城
的一个序列,其中每个函数定义在某一城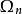 内,且在该域内调和。设
内,且在该域内调和。设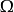 为这样的一个域,它的每一点具有一个邻域包含于除有穷个以外的所有
为这样的一个域,它的每一点具有一个邻域包含于除有穷个以外的所有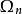 中,并设在这一邻域中,当n足够大时,有
中,并设在这一邻域中,当n足够大时,有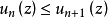 。那么这里只有两种可能:或者是
。那么这里只有两种可能:或者是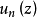 在
在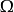 的每个紧致子集上一致地趋于
的每个紧致子集上一致地趋于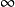 ,或者是
,或者是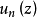 在紧致集上一致收敛于
在紧致集上一致收敛于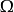 内的一个调和极限函数
内的一个调和极限函数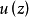 。
。
最简单的情形是函数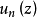 在
在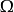 内均为调和,并组成一个非降序列。不过,有很多应用说明这种情形不够普遍。
内均为调和,并组成一个非降序列。不过,有很多应用说明这种情形不够普遍。
为了证明这一定理,先设至少对于一点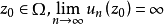 。根据假设,可以找到一个r和m,使得对于
。根据假设,可以找到一个r和m,使得对于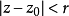 及
及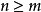 ,函数
,函数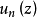 都是调和的,并组成一个非降序列,如果将不等式(3)的左边应用于非负函数
都是调和的,并组成一个非降序列,如果将不等式(3)的左边应用于非负函数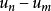 ,则知
,则知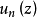 将在圆盘
将在圆盘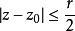 中一致地趋于
中一致地趋于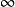 ,另一方面,如果
,另一方面,如果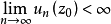 ,应用不等式的右边同样可证明
,应用不等式的右边同样可证明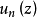 在
在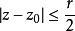 上有界。因此,在其上
上有界。因此,在其上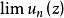 分别为有穷及无穷的两个集都是开集,而由于
分别为有穷及无穷的两个集都是开集,而由于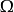 是连通的,故必有一个集是空集。只要
是连通的,故必有一个集是空集。只要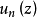 的极限在单一点上是无穷大,则它必恒等于无穷大。至于一致性,可用海涅一博雷尔引理来证明。
的极限在单一点上是无穷大,则它必恒等于无穷大。至于一致性,可用海涅一博雷尔引理来证明。
在相反的情形,极限函数 是到处均为有穷的,我们现在只要证明其收敛是一致的即可。应用上面的同样记法,对于
是到处均为有穷的,我们现在只要证明其收敛是一致的即可。应用上面的同样记法,对于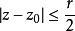 及
及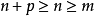 ,有
,有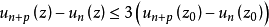 ,因此,在
,因此,在 点收敛就意味着在
点收敛就意味着在 的一个邻域中一致收敛,再应用海涅-博雷尔引理可知在每个紧致集上收敛是一致的。至于极限函数的调和性,则可从
的一个邻域中一致收敛,再应用海涅-博雷尔引理可知在每个紧致集上收敛是一致的。至于极限函数的调和性,则可从 能用泊松公式来表示这一点而得证。
能用泊松公式来表示这一点而得证。
设E是包含于域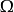 中的一个紧致集,证明,存在一个只依赖于E及
中的一个紧致集,证明,存在一个只依赖于E及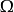 的常数M,使得
的常数M,使得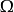 中的每个正调和函数
中的每个正调和函数 ,对于任意两点
,对于任意两点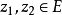 ,满足不等式
,满足不等式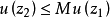 。2
。2
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国