[科普中国]-高阶奇点托姆定义

高阶奇点托姆定义是高阶奇点的一种定义，是对一阶奇点进一步分类的一种方法。在一阶奇点分类不足以充分刻画其性质时可做更细微的分类方法。

简介高阶奇点托姆定义是高阶奇点的一种定义，对一阶奇点进一步分类的一种方法。在一阶奇点分类不足以充分刻画其性质时可做更细微的分类方法，奇点的 分类（即一阶奇点）还不够精细，映射在两个同一类型 的奇点上，可能具有极不同的性态。因此有必要对奇点做进一步的分类，托姆(Thom,R.)提出了一个构想。

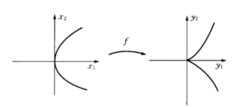
托姆构想先从一个具体的例子来看托姆的思想，考虑映射f如下:

f 的雅可比矩阵为

根据 型奇点的定义， 为平面上的抛物线，除去抛物线 之外，整个平面的其余部分为 。

抛物线 是 R2上的光滑曲线，因此可以考虑 f 在 上的限制映射 ，此时，原点是 的 型奇点，奇点集 记为 。抛物线 除原点外其他点皆为 型奇点，奇点集 记为 。

这样就把 f 的奇点集 进一步分为两类奇点 和 。

对一般情况，托姆的构想如下：设 f:M→N 是光滑映射，若奇点集 是 M 的子流形，则可以考虑 f 在 上的限制映射 的 型奇点集记为 ，即 ，称为 f 的 型奇点，这是二阶奇点，若 还是 M 的子流形，则可以仿照上述构造三阶奇点

最一般的情形，可以归纳构造如下：对于任意非负整数集 ，若

已确定并且是 M 的子流形，则 就记为 ，即 的 型奇点称为 型奇点。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学