[科普中国]-局部化原理

基本介绍

**(黎曼局部化原理)**设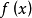 是在区间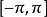 上按一段连续的以 为周期的周期函数，A是一常数，则从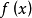 导出的傅里叶级数

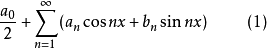在定点x处收敛于A的充要条件是： 对于任意 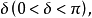都有

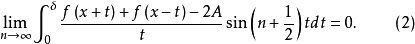注意(2)式（和下面的(3)）式中的积分是在 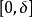上取的，因此只涉及到 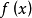在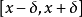 这一区间上的值，和 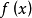在这一区间以外的值无关。而 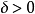又是任意的，因此黎曼局部化原理(和下面命题1)说明从 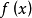导出的傅里叶级数(1)在定点x处是否收敛(于某常数A)，只和 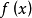在点x附近的性质有关，这就是黎曼局部化原理(和下面命题1)称为局部化原理的原因2。

相关命题与定理如果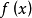 是在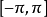 上按段连续的以 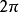为周期的函数，A是一常数，则从 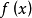导出的傅里叶级数(1)在x点收敛于A的充要条件是：对子任意 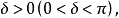都有

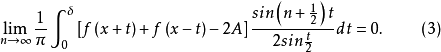
为了把（3）式写成更便于应用的形式，注意

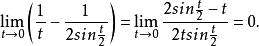所以对于固定的x，

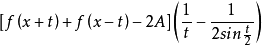是 的在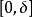 上按段连续的函数，于是由黎曼引理，

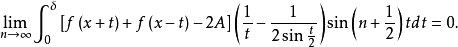从而，(3)式成立与

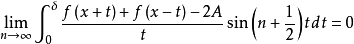成立是等价的，于是命题1可改进为黎曼局部化原理2。

收敛性定理根据黎曼局部化原理，立即可得下述收敛性定理：

如果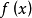 是在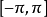 上按段光滑的以 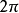为周期的周期函数，则从 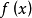导出的傅里叶级数(1)是处处收敛的，其和是 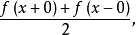即有

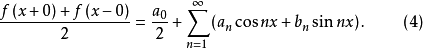注意，如果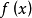 在点x 处连续，则 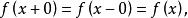因此当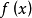 满足收敛性定理的条件时，从它导出的传里叶级数必在 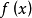的一切连续点处收敛于 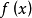2。