[科普中国]-球面定理

三维流形几何

三维流形几何(the geometries of 3-mani-folds)是研究三维流形上的常曲率的几何。

至今可以用三种方式来谈论几何，第一种：古典的欧氏几何，在其中考虑点、线、面、角、长度等以及它们之间的相互关系，而且这种方法对于非欧几何也适用；第二种:微分几何；第三种是克莱因意义下的几何，即考虑空间X与其上的一个可迁变换群G，所谓几何(X,G)即考虑X在G之下的那些不变性.当然这三者只是立论不同而已，其内容有时是共通的.在这里所论的几何正是克莱因意义之下的几何.由于流形M与它的泛覆叠空间X之间有相同的度量，所以为了讨论流形M上的局部齐性度量，只须讨论X上的齐性完备度量即可，其中G=Isomπ/2。曾有许多作者试图将Berger-Klingenberg拓扑球面定理改进为微分球面定理。最近，S.Brendle和R.Schoen发展了Ricci流的方法，证明了截面曲率逐点拼挤条件下的微分球面定理这是黎曼几何最近几年发展的一项重要结果。最近，获得了数量曲率拼挤条件下常曲率空间形式中完备子流形的最佳微分球面定理。研究人员曾证明，在截面曲率拼挤条件下，常曲率空间形式中的紧致子流形拓扑同胚于球面。4

**定理1：**设M是曲率为正常数c的n+p维完备单连通空间形式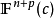中n≥4维紧致定向的子流形。若M的截面曲率满足：

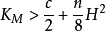则M拓扑同胚于n维球面。

**定理2：**设M是曲率为正常数c的n+p维完备单连通空间形式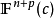中n≥4维紧致定向的子流形。若M的截面曲率满足：

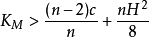那么M微分同胚于标准球面。

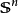**定理3：**设M是欧式空间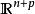中n维紧致定向的子流形。若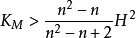，若M拓扑同胚于球面。特别地，当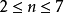时，M微分同胚于标准球面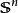。5