[科普中国]-规范正交基

简介

在数学中，特别是线性代数，具有有限维度的内积空间V的正交基是其向量的基，即它们都是单位向量并且彼此正交。例如，欧几里德空间Rn的标准基是正交基，其中内积是向量的点积。在旋转或反射（或任何正交变换）下的标准基的映射也是正交的，并且Rn的每个正交基都以这种形式出现。1

规范正交基(orthonormal basis)完备的规范正交系。设H为希尔伯特空间，H的完备的规范正交系F称为H的规范正交基或正规正交基。F的基数称为希尔伯特空间H的维数。两个维数相同的希尔伯特空间是等距同构的。规范正交基实际上是欧几里得空间中规范正交基的一种推广。

对于一般的内积空间V，可以使用正交基数来定义V上的归一化正交坐标。在这些坐标下，内积变为向量的点积。因此，正交基的存在减少了有限维内部空间的研究，以研究点阵积分下的Rn。每个有限维的内积空间都有一个正交基，这可以从任意的基础上使用格拉姆 - 施密特方法获得。

在功能分析中，正交基的概念可以推广到任意（无限维）内积空间（或希尔伯特前空间）。给定希尔伯特前空间H，H的正交基是正交的向量集合，其特征在于H中的每个向量可以被写为基于向量的无限线性组合。在这种情况下，正交基础有时被称为H的希尔伯特基。注意，在这个意义上，正交基通常不是哈默尔基础，因为需要无限线性组合。具体来说，基础的线性跨度必须在H中是致密的，但它可能不是整个空间。

如果我们进入希尔伯特空间，那么与正交基数相同的线性跨度的非正交矢量集合可能根本不是基。例如，间隔[-1,1]上的任何平方可积分函数可以被表示（几乎在任何地方）作为勒布雷多项式的无限和（一个独立基础），但不一定作为单项式xn的无限和。2

举例向量集合{e1 =（1,0,0），e2 =（0,1,0），e3 =（0,0,1）}（标准基）形成R3的正交基。

证明：一个简单的计算表明，这些向量的内积等于零，⟨e1，e2⟩=⟨e1，e3⟩=⟨e2，e3⟩= 0，它们的维度都等于1，|| e1 || = || e2 || = || e3 || = 1。这意味着{e1，e2，e3}是正交集合。 R3中的所有向量（x，y，z）可以表示为基向量的和：

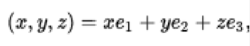
所以{e1，e2，e3}一定是R3的基。还可以表明，围绕轴线穿过原点旋转或者通过原点反射的平面的标准基础形成R3的正交基。

基本式如果B是H的正交基，则H的每个元素x可以被写为

当B是正交的时候，这就简化成

x的范数的平方可以给出

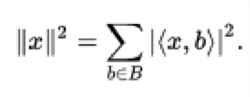
即使B是不可数的，这个总和中很多是非零的，因此表达式是明确的。 这个总和也称为x的傅立叶扩展，公式通常称为Parseval的身份。

不完全正交基给定希尔伯特空间H和H中相互正交向量的集合S，我们可以取包含S的H的最小闭合线性子空间V，然后S将是V的正交基；当它是一个完整的正交集合时，其当然可以小于H本身，是不完整的正交集，或者是H。3

存在性使用Zorn的引理和Gram-Schmidt过程（或更简单的排序顺序和无限次递归），可以显示每个希尔伯特空间都承认了一个基础，从而得到了一个正交基础；此外，相同空间的任何两个正交基座具有相同的基数（这可以以类似于向量空间的通常维度定理的证明的方式被证明，并且取决于较大的基础候选是可数的还是单独的情况） 不）。 当且仅当它承认可数的正交基础时，希尔伯特空间是可分离的。 （可以证明这最后一个陈述，而不使用公理的选择）