[科普中国]-分次环论

简介

分次环与模最初发展的主要动力是交换代数几何中的射影代数簇，并形成代数几何研究中的基本方法之一自20世纪70年代以来，(群)分次环和模的发展进人了一个崭新的时期，主要来自非交换代数几何及群表示理论的推动.群分次环理论非常活跃且富有成果，在这一发展阶段中代表人物有奥西塔因(F. Van.Oystaeyen)、纳斯塔西库(C.Nastasescu )、达第(E. C.Dade 、蒙哥马利(S.Montgomery )、科恩(Cohen, M.)和帕斯曼(D. S.Passman)等.群分次环以其与众多数学分支的密切联系而引起人们的极大兴趣.

实例例如:

1.相伴于滤子化环的Z分次环理论是李代数、代数几何尤其是层理论、微分方程尤其是微分算子环等理论研究中的有力工具。

2.非交换环的任意群分次的理论在群作用于环及不动点(环)、群表示理论尤其是稳定克利福德理论等发挥了重要的作用。

3.非交换环的有序群分次的理论及由此而产生的分次序理论是数论、代数表示论、非交换代数几何、维数理论和环理论的一个重要的基本成分。

4一般群分次理论与霍普夫代数、冯·诺伊曼代数等理论有着深刻的联系。

值得一提的是，分次环的理论固然重要，而更重要的是分次环的研究方法，这一点可以从分次环的广泛而富有意义的应用中看出1。

第一个属性让

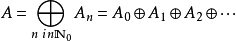成为一个分级的环。任何因素的元素 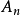分解的被称为同质元件的程度Ñ。每个元件一个的可以写成的总和 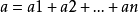与所有一个ai不同的均匀的元件Ai。这一个ai被称为均一组分的a。

一些基本属性是：

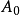是A的一个子环;特别地，加法度量0和乘法式1是零度的齐次元素。

交换环形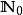 环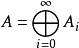 是一个诺埃利亚环当然如果 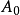是Noetherian，A是有限生成的代数 。

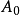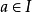一个理想的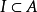 如果每一个元素都是同质的，其同质成分也属于 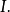（等价地，它们是A的分级子模块;参见§分级模块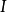）。 与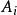 被称为均质部件的 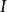。齐次理想是其均质部分的直接和2。

如果我是A的同质理想，那么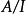 也是一个分级的环，并已分解

分级模块模块理论中的相应思想是一个分级模块，即分级环A上的左模块M也是这样

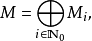
和

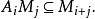
例如：一个渐变向量空间是一个字段上的渐变模块的示例（字段具有平凡的分级）。

例如：分级环是一个分级模块。当且仅当它是分级子模块时，分级环中的理想是均匀的。分级模块的歼灭者是一个同质的理想。

例如：给定交换环R和R模块M的理想I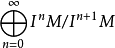， 是相关分级环上的分级模块 。

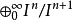一种态度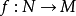 在分级模块之间，称为分级态射，是一种尊重分级的基本模块的态射；即 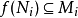。甲分级子模块是一个辅助模块是在自己的权利的分级模块，并且使得集合论夹杂物是分级模块的态射。显式地，分级模块N是M的分级子模块，当且仅当它是M的子模块并且满足 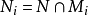。内核和渐变模块的态射图像是分级的子模块。

备注：从渐变环到渐变环的渐变态，其图像位于中心，这与将渐变代数的结构赋予后一个环相同。

由于分级模块M,时，ℓ的捻合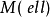 是由...定义的分级模块 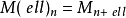。（参见塞尔的代数几何中的扭曲捆）

设M和N为分级模块。如果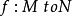 是模块的态射，然后˚F据说有度d是否 。微分几何中的微分形式的外部导数是这样的具有次数1的态射的例子3。