预备知识线性空间
设 X 是一个非空集,K 是复(或实)数域,如果满足条件:
(1)X 是一加法交换群,即对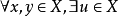 ,记作
,记作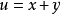 称为
称为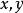 之和,适合
之和,适合
①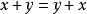 ;
;
② ;
;
③ 存在唯一的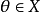 ,对
,对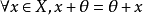 ;
;
④ 对任意的 ,存在唯一的
,存在唯一的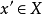 ,使得
,使得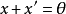 ,记作
,记作 为
为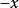 ;
;
(2)定义数域 K 中的数 与
与 的数乘运算,即
的数乘运算,即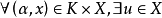 ,记作
,记作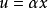 称为
称为 对
对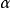 的数乘,适合
的数乘,适合
①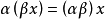 ;
;
② ;
;
③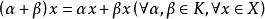 ;
;
④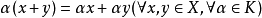 ;
;
则称 X 为一复(或实)线性空间。1
线性空间上的范数若线性空间 X 上的一个非负值函数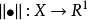 满足:
满足:
(1)正定性: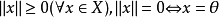 ;
;
(2)三角不等式: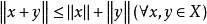 ;
;
(3)齐次性: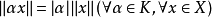 ;
;
则称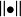 为线性空间 X 上的一个范数。1
为线性空间 X 上的一个范数。1
赋范线性空间当赋准范数的线性空间中的准范数是范数时,称该空间为赋范线性空间。1
一个范数比另一范数强设在线性空间 X 上给定了两个范数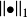 和
和 ,若有
,若有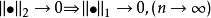 ,则称
,则称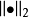 比
比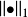 强。1
强。1
为了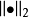 比
比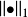 强,必须且只需存在常数 C>0 ,使得
强,必须且只需存在常数 C>0 ,使得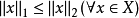 。1
。1
定义在许多分析问题中,引进范数或引进距离是为了研究一种收敛性。因此,如果我们关心的只是按照一定意义的收敛性而不是距离本身的大小,那么在空间上我们就可以认为决定同一收敛性的不同范数是等价的。等价范数是同一个线性空间上的两个范数之间的一种关系。
数学表示设在线性空间 X 上给定了两个范数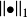 和
和 ,如果
,如果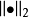 比
比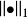 强,并且
强,并且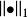 比
比 强,则称
强,则称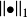 和
和 等价。1
等价。1
等价的意义Banach空间中的两范数等价,则说明这两个范数的Banach空间拓扑性质相同,特别是 B 空间中序列的收敛性、集合的有界性、线性算子的有界性、以及一族算子的一致有界,在从一个范数变化到另一个范数时,都是不变的。2
因此,与在同一个集合 X 上可以定义不同的距离使 X 成为不同的度量空间一样,在同一个线性空间 E 上,也可以定义不同的范数,使E构成不同的赋范线性空间。3
基本结论结论1(等价范数定理)设在线性空间 X 上给定了两个范数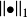 和
和 ,若存在两个常数
,若存在两个常数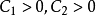 ,使得
,使得
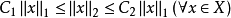
则有两范数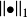 和
和 等价。1
等价。1
结论2设 X 是一个有穷维线性空间,若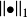 和
和 都是 X 上的范数,则必有常数
都是 X 上的范数,则必有常数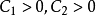 ,使得:
,使得:
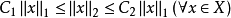
该结论表明:具有相同维数的两个有穷维线性赋范空间在代数上是同构的,在拓扑上是同胚的。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国