概念
赋范线性空间(normed linear space)是在线性空间中引进一种与代数运算相联系的度量,即由向量范数诱导出的度量。赋范线性空间称为Banach空间,是指由范数导出的度量是完备的。
定义:设 是线性空间,函数
是线性空间,函数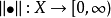 称为
称为 上定义的一个范数,如果满足:
上定义的一个范数,如果满足:
(1)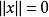 当且仅当
当且仅当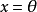 ;
;
(2)对任何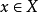 及
及 ,
,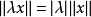 ;
;
(3)对任意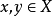 ,
,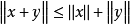 。
。
称二元体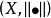 为赋范线性空间。
为赋范线性空间。
在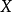 是赋范线性空间时,由范数导出的度量为
是赋范线性空间时,由范数导出的度量为
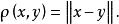 此时
此时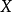 在此度量意义称为度量空间。所以,赋范线性空间是一种特殊的度量空间。点列
在此度量意义称为度量空间。所以,赋范线性空间是一种特殊的度量空间。点列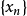 收敛于
收敛于 ,即
,即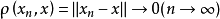 ,有时称这种收敛为依范数收敛。1
,有时称这种收敛为依范数收敛。1
性质性质1:设 是赋范线性空间,
是赋范线性空间,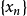 ⊂
⊂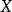 ,
,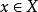 ,若
,若 ,则
,则 是有界点列。
是有界点列。
证: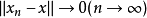 ,对
,对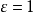 ,存在自然数
,存在自然数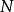 ,当
,当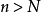 时,
时,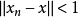 。于是
。于是
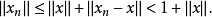 令
令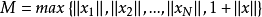 ,那么对一切自然数
,那么对一切自然数 ,均有
,均有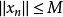 ,即
,即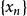 有界。证毕。
有界。证毕。
性质2:设 中点列
中点列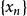 ,
,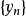 及数域
及数域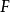 中数列
中数列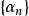 满足
满足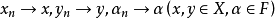 ,则
,则
(1)加法连续: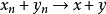 ,即
,即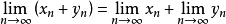 ;
;
(2)数乘连续: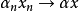 ,即
,即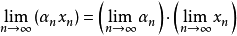 。
。
证:(1)由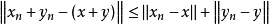 ,得
,得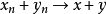 。
。
(2)因 ,由性质1,
,由性质1, 有界,所以存在常数
有界,所以存在常数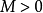 ,满足
,满足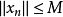 。于是
。于是
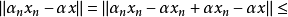
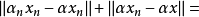
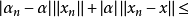
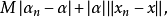 故
故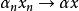 。证毕。1
。证毕。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国