[科普中国]-半本原环

半本原环亦称半单环，一类重要的环。若环R的雅各布森根J(R)=0，则R称为半本原环，又称雅各布森半单环。一个环R是半本原环的充分必要条件是R为本原环的亚直和。

简介半本原环亦称半单环，一类重要的环。若环R的雅各布森根J(R)=0，则R称为半本原环，又称雅各布森半单环。一个环R是半本原环的充分必要条件是R为本原环的亚直和。1

左本原环[left primitive ring]

对于环 R ，若存在忠实单左 R 模，则称 R 为左本原环。左阿廷环为左本原环当且仅当其为单环，当且仅当其为素环。

设 M 是除环 D 上的右向量空间，R为End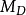（ ）的子环。若对于任意正整数 n 及 M 中任意两组元素 及 其中 是D- 线性无关的，都有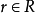 使得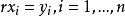 则称 R 是 M 上的稠密线性变换环（dense ring of linear transformations）。

雅各布森稠密性定理（Jacobson's density theorem）：

设 R 为左本原环，M 为忠实单左 R 模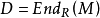， ，则 R 是 上的稠密线性变换环。

若环 R 的理想 P 满足 R/P 为左本原环，则称 P 为 R 的左本原理想（left primitive ideal）。类似地，可定义右本原环（right primitive ring）、右本原理想（right primitive ideal）。

左（右）本原理想恰为一左（右）单模的零化子。若环 R 没有左（右）本原理想（或左（右）单模），则 R 的所有左（右）本原理想的交恰为环 R 的雅各布森根。若环 R 的雅各布森根为零，则称 R 为半本原环（semiprimitive ring）。环 R 为半本原环当且仅当 R 为左（右）本原环的次直积。

雅各布森根在抽象代数之分支环理论中，一个环R的雅各布森根（Jacobson radical）是R的一个理想，包含在某种意义上“与零接近”的那些元素。雅各布森根是雅各布森(Jacobson,N.)于1945年引入的。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学