半素理想(semiprime ideal)是与半素环密切相关的概念。环R的理想Q,若对R的任意理想A和某个自然数n,有An⊆Q,就恒有A⊆Q,则称Q为R的半素理想。它等价于,对R中任意元素x,若xRx⊆Q,则x∈Q1。
定义设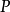 是半环
是半环 的理想,若对于
的理想,若对于 的任意理想
的任意理想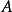 ,由
,由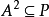 必推得
必推得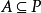 ,则称
,则称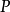 为
为 的半素理想2。
的半素理想2。
相关概念及定理命题1设P是半环S的理想,则P是半素理想的充分必要条件是对任意理想A,由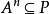 必推得
必推得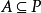 ,其中n为某个自然数2。
,其中n为某个自然数2。
定义2设M是半环S的一个子集,若对任意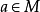 ,存在
,存在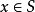 使得
使得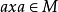 ,称M为S的一个n-系统。
,称M为S的一个n-系统。
命题3设P是半环S的理想,则P是半素的当且仅当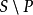 是S的一个n-系统。
是S的一个n-系统。
定理4设P是半环S的理想,则下列等价:
1) P是半素理想;
2) 设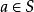 ,若
,若 ,则
,则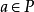 ;
;
3) 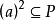 必推得
必推得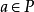 ,其中(a)为由a生成的主理想;
,其中(a)为由a生成的主理想;
4) 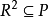 必推得
必推得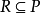 ,其中R是S的右理想;
,其中R是S的右理想;
5) 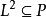 必推得
必推得 ,其中L是S的左理想。
,其中L是S的左理想。
定义5设P是半环S的理想,若对任意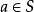 ,由
,由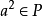 必推得
必推得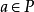 ,称P为S的完全半素理想。
,称P为S的完全半素理想。
易知,若P是半环S的完全半素理想,则由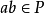 必推得
必推得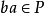 。
。
定理6设P是半环S的素理想,则P是完全素理想的充分必要条件是P是完全半素理想。
推论7设S是交换半环,则S的素理想、完全素理想与完全半素理想三个概念是一致的。
定理8设N是半环S的理想,则
1) 若P是S的素理想,则 是N的素理想;
是N的素理想;
2) 若P是S的半素理想,则 是N的半素理想。
是N的半素理想。
**证明:**1) 记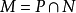 ,则M是N的理想。设
,则M是N的理想。设 ,若
,若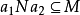 ,则
,则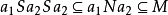 ,于是
,于是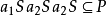 ,从而
,从而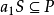 或
或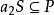 ,进而,
,进而,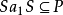 或
或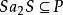 ,得到
,得到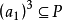 或
或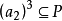 ,推得
,推得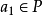 或
或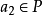 ,这样
,这样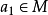 或
或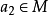 ,即M是N 的素理想。
,即M是N 的素理想。
2) 记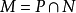 ,设
,设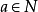 ,若
,若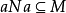 ,则
,则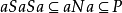 ,于是,
,于是,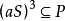 ,得
,得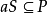 ,进而
,进而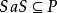 ,从而
,从而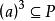 ,所以
,所以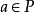 ,即
,即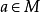 ,故M是N的半素理想。
,故M是N的半素理想。
定义9若{0}是半环S的素(半素)理想,则称S为素(半素)半环。
定理10设P是半环S的强理想,则下列等价:
1) P是素理想;
2) 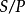 是素半环;
是素半环;
3) 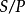 中任意两个非零理想之积非零。
中任意两个非零理想之积非零。
定理11设P是半环S的强理想,则下列等价:
1) P是半素理想;
2) 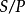 是半素半环;
是半素半环;
3) 若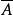 是
是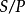 的非零理想,则
的非零理想,则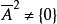 ;
;
4) 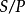 不含非零幂零理想;
不含非零幂零理想;
5) 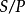 不含非零幂零单侧理想,即
不含非零幂零单侧理想,即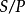 是有效半环。
是有效半环。
定理10、11中的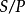 都是指S关于同余的商半环,这两个定理的证明只要注意到
都是指S关于同余的商半环,这两个定理的证明只要注意到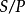 的理想(单侧理想)的形式是且只是形如
的理想(单侧理想)的形式是且只是形如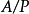 ,其中
,其中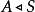 ,且
,且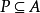 ,就不难了2。
,就不难了2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国