[科普中国]-核型空间

概念

核型空间是一类局部凸空间。局部凸空间X称为核型空间，如果对零元的任何均衡凸邻域V，存在另一零元的均衡凸邻域U⊂V，使得典型映射T：XV→XU是核映射。这里，XU是商空间(X，PU(·))/{x|PU(x)=0}，而XV是商空间(X，PV(·))/{x|PV(x)=0}的完备化空间，PU(·)及PV(·)是由U和V各自产生的闵科夫斯基泛函。巴拿赫空间为核型空间的充分必要条件是该空间为有限维的。核型空间在分析学中有非常重要的应用，是格罗腾迪克(Grothendieck，A.)于1955年首先引入的。1

拓扑线性空间拓扑线性空间是泛函分析的重要分支，又称之为拓扑向量空间，它是具有拓扑结构的线性空间，是赋范线性空间概念的推广。

20世纪初，法国数学家弗雷歇在引入距离空间，并用距离概念来统一过去分析学中的许多重要收敛时，就知道[a，b]上一列函数的“点点收敛”概念是不能用距离收敛来描述的。20世纪30年代以来，泛函分析中大量应用弱收敛、弱拓扑，它们都不能用距离来描述。这就很自然地把赋范线性空间理论发展成更一般的拓扑线性空间理论，其中最主要的成就是局部凸拓扑线性空间理论。这一分支的发展是与一般拓扑学的发展紧密联系在一起的。拓扑学方法在这里发挥了极其重要的作用，法国数学家勒雷和波兰数学家绍德尔所推广的不动点定理就是有力的例证之一。1935年以后，经过十多年的努力，这一分支终于形成，它的许多结果不仅在泛函分析中有着广泛的应用，而且为其他分析学科的深入研究提供了基本框架和有力的工具。

局部凸空间局部凸空间是最重要的一类拓扑线性空间。设E是拓扑线性空间，如果E中存在由均衡凸集组成的零元的邻域基，就称E是局部凸的拓扑线性空间，简称局部凸空间，而E的拓扑称为局部凸拓扑。零元的每个均衡凸邻域V的闵科夫斯基泛函pV(x)是E上的连续半范数。反之，设{pλ|λ∈Λ}是E上一族半范数，E上使pλ(λ∈Λ)均为连续的最弱拓扑是局部凸的，且零元的均衡凸邻域基由下面形式的集组成：

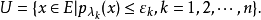
这个局部凸拓扑称为由半范数族{pλ}确定的局部凸拓扑。如果对任何x∈E(x≠0)，都存在λ∈Λ使pλ(x)≠0，则{pλ|λ∈Λ}确定的局部凸拓扑是豪斯多夫拓扑。通常局部凸空间都指豪斯多夫局部凸空间。E中的定向半序点列{xα}收敛于x∈E等价于对每个λ∈Λ，pλ(xα-x)→0。设E1是由另一半范数族{qβ}确定的局部凸空间，则使线性映射T：E→E1连续的充分必要条件是，对任意的qβ，总存在有限个λ1，λ2，…，λn∈Λ和常数c，使不等式：

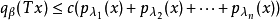
对一切x∈E成立。

局部凸空间的完备化空间也是局部凸的。根据哈恩-巴拿赫泛函延拓定理，局部凸空间上存在足够多的非零连续线性泛函.正因为如此，局部凸空间理论成为拓扑线性空间理论中最重要的部分.

关于局部凸空间理论的发展大约是始于迪厄多内(Dieudonné，J.)和施瓦兹(Schwarz，L.)在1949年的工作，它的一个主要推动力是分布理论，即广义函数理论。

商空间商空间是一个线性空间模一个子空间所得的线性空间。设V是域P上的线性空间，W是V的子空间，对V中每一元α，定义α+W={α+β|β∈W}，设V-={α+W|α∈V}，利用V的加法及P与V的纯量乘法，可以在V'内引入如下的加法及P与V'的纯量乘法：

(α+W)+(β+W)=(α+β)+W，

k(α+W)=kα+W (k∈P).

这样的定义是完全确定的，而且V-关于这样定义的运算构成域P上的一个线性空间，称为V对子空间W的商空间，记为V/W。例如，若V是P上5维线性空间，α1，α2，α3，α4，α5是基，W是由α1，α2生成的子空间，则V/W是由三个元素α3+W，α4+W，α5+W生成的商空间，而且这三个元素正好是V/W的基。一般地，若dim V/W有限，则称其为W关于V的余维数，记为Codim W。2

人物简介——格罗腾迪克数学家。出生于德国柏林，父亲为俄国人，母亲为德国人，13岁时逃亡到法国，长期保持无国籍身份。早年没有受过正规教育，第二次世界大战后才到巴黎高等师范学校和法兰西学院去听课。1960—1969年任法国高等科学研究所教授。他热衷于和平主义和环境保护的宣传，1970年当他得知数学研究受军方资助时，即辞职回乡务农。

格罗腾迪克在泛函分析和代数几何领域都有重要贡献。1952—1955年，他在线性拓扑空间理论的研究中引进了拓扑张量积和核空间的概念，这些工作曾受到数学界的广泛注意。1955—1957年，他对阿贝尔范畴理论进行了系统研究，并发展了同调代数理论。1957年开始，他转向了代数几何及其在数论中的应用的研究。他在证明广义黎曼-罗赫定理时，第一次给出了概型X的向量丛的格罗腾迪克群，并引入了代数K理论。1958年开始，他建立了代数几何中的概型理论，把代数几何和代数数域的算术统一了起来。这一理论对交换代数的发展也起了巨大推动作用。概型理论在证明韦伊猜想和莫德尔猜想中起了重要作用。1966年，格罗腾迪克获菲尔兹奖章;1988年，获瑞典皇家科学院克罗福特奖。他曾与他人合作写了两部多卷本的关于概型和基础群等的书，另外他还著有《拓扑向量空 间》(Espaces VectorieleTopologiques，1954)、《代数几何基础》(Fondements de la Geometrie Algebrique，1962)等。3