[科普中国]-可赋范拓扑线性空间

可赋范拓扑线性空间（normable topological linear space）是指可用范数来刻画拓扑的拓扑线性空间。

简介可赋范拓扑线性空间是指可用范数来刻画拓扑的拓扑线性空间。

设E是拓扑线性空间，如果E上还存在一个范数||·||，使||·||导出的拓扑与E中原来的拓扑相同，则称E是可赋范的。1

判定拓扑线性空间可赋范的充分必要条件是满足下面三条：

1.E满足T0公理；

2.E是局部凸的；

3.E是局部有界的。

上述充分必要条件是柯尔莫哥洛夫于1934年给出的，也是最早得到的有关拓扑线性空间理论的一个结果。

拓扑线性空间设X为实数域或复数域K上的线性空间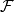，是X上的拓扑，如果

（1）加法是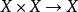的连续映射；

（2）数乘是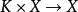的连续映射；

则称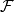是X上的向量拓扑或线性拓扑，称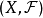为拓扑线性空间或拓扑向量空间。

注：1）零元的均衡的邻域全体组成零元的邻域基。

2）满足T1分离公理的拓扑线性空间是完全正则的。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学