基础概念定义
设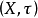 是拓扑线性空间,如果X中存在由有界集组成的局部基,则称X是局部有界的拓扑线性空间,简称为局部有界空间;如果X中存在由凸集组成的局部基,则称X是局部凸拓扑线性空间,简称为局部凸空间。我们知道,度量空间是拓扑空间;反之,拓扑空间要在一定条件下才能定义与拓扑相一致的度量而成为度量空间,拓扑空间X称为可度量化的,如果在X上有度量
是拓扑线性空间,如果X中存在由有界集组成的局部基,则称X是局部有界的拓扑线性空间,简称为局部有界空间;如果X中存在由凸集组成的局部基,则称X是局部凸拓扑线性空间,简称为局部凸空间。我们知道,度量空间是拓扑空间;反之,拓扑空间要在一定条件下才能定义与拓扑相一致的度量而成为度量空间,拓扑空间X称为可度量化的,如果在X上有度量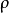 ,使由
,使由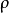 导出的度量拓扑就是X上的拓扑。2
导出的度量拓扑就是X上的拓扑。2
相关概念设X是数域K上的线性空间,又是度量空间,度量为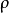 。
。
(1)若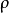 满足
满足
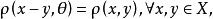 则称
则称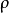 为平移不变度量。
为平移不变度量。
(2)设由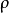 导出拓扑
导出拓扑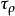 ,若
,若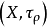 为拓扑线性空间,则称
为拓扑线性空间,则称 为度量线性****空间。
为度量线性****空间。
设X为数域K上线性空间,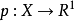 为泛函,若p满足(N2)(绝对齐性)与(N3)(三角形不等式),则称p为X上的半范数;若p为X上半范数,则称
为泛函,若p满足(N2)(绝对齐性)与(N3)(三角形不等式),则称p为X上的半范数;若p为X上半范数,则称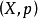 为赋半范空间,若p满足(N1)(正定性)与(N3)以及(N2)*准齐性
为赋半范空间,若p满足(N1)(正定性)与(N3)以及(N2)*准齐性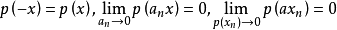 ,其中
,其中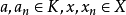 .则称p为X上的准范数;若p为X上的准范数,则称
.则称p为X上的准范数;若p为X上的准范数,则称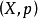 为赋准范空间,易知范数必是半范数,反之不真.半范数比范数仅少了一个正定性公理。取
为赋准范空间,易知范数必是半范数,反之不真.半范数比范数仅少了一个正定性公理。取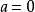 ,由绝对齐性得
,由绝对齐性得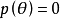 ,在三角形不等式中令
,在三角形不等式中令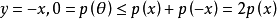 ,得到
,得到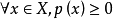 .但
.但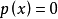 未必蕴涵
未必蕴涵 。
。
Minkowski泛函
设X是线性空间,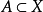 为吸收集,则称X上的泛函
为吸收集,则称X上的泛函
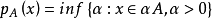 为A的Minkowski泛函。
为A的Minkowski泛函。
可赋范
设X是拓扑线性空间.若X上可定义范数,使范数诱导的度量拓扑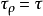 ,则称X是可赋范的。
,则称X是可赋范的。
相关性质定理命题1设X为数域K上线性空间,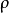 为X上平移不变度量,则
为X上平移不变度量,则 为度量线性空间的充分必要条件是:对每个
为度量线性空间的充分必要条件是:对每个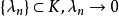 。时有
。时有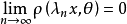 。我们知道在第一可数的拓扑空间中,收敛可以用点列而不需用网来描述,度量空间是第一可数的。定理1指出,对于Hausdorff的拓扑线性空间来说,第一可数性决定了可度量性。2
。我们知道在第一可数的拓扑空间中,收敛可以用点列而不需用网来描述,度量空间是第一可数的。定理1指出,对于Hausdorff的拓扑线性空间来说,第一可数性决定了可度量性。2
定理1(度量化定理)设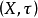 是Hausdorff的拓扑线性空间,若
是Hausdorff的拓扑线性空间,若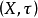 还满足第一可数公理(即具有可数局部基),则
还满足第一可数公理(即具有可数局部基),则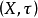 可度量化,且X上有平移不变度量
可度量化,且X上有平移不变度量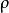 ,使
,使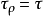 。
。
推论局部有界空间必具有可数局部基,从而Hausdorff的局部有界空间必可度量化。
证明: 设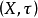 是局部有界空间,
是局部有界空间,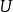 是
是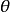 的有界邻域,则
的有界邻域,则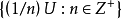 就是
就是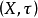 的局部基,故
的局部基,故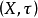 满足第一可数公理,由定理1可知推论成立,证毕。
满足第一可数公理,由定理1可知推论成立,证毕。
命题2设X为数域K上线性空间,p是X上的一个半范数或准范数,则
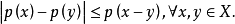 于是赋准范空间与赋半范空间都是拓扑线性空间,其半范数与准范数是连续的。
于是赋准范空间与赋半范空间都是拓扑线性空间,其半范数与准范数是连续的。
命题3赋准范空间是度量线性空间。
命题4设p是线性空间X上的一个半范数,则
(1)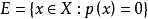 是X的线性子空间;
是X的线性子空间;
(2)对任何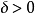 ,集
,集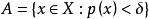 是X中的平衡吸收凸集。
是X中的平衡吸收凸集。
定理2设A是拓扑线性空间X中的吸收凸子集,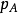 是A的Minkowski泛函,
是A的Minkowski泛函,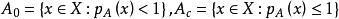 ,则
,则
(1)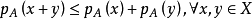 ;
;
(2)若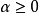 ,则
,则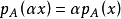 ;
;
(3)若A还是平衡的,则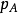 是半范数;
是半范数;
(4)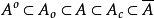 ;
;
(5)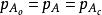 ;
;
(6)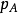 连续
连续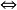
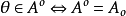 ;
;
(7)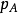 连续
连续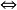
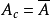 。
。
定理3设X是线性空间,在X上给定一族半范数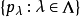 .令
.令
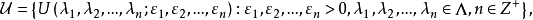 其中
其中
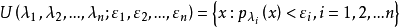
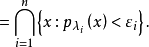 则存在唯一拓扑
则存在唯一拓扑 使
使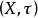 为局部凸空间且
为局部凸空间且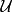 为其局部基,X是Hausdorff空间当且仅当
为其局部基,X是Hausdorff空间当且仅当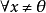 有
有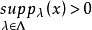 ,称
,称 为由半范数族
为由半范数族 生成的拓扑。2
生成的拓扑。2
推论1赋范空间是Hausdorff的局部凸空间。
推论2设线性空间X上的拓扑由给定的一列半范数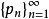 生成且满足
生成且满足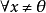 有
有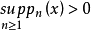 ,则X是局部凸的度量线性空间。
,则X是局部凸的度量线性空间。
定理4设X是局部凸空间,则它的拓扑 必可由一族连续半范数
必可由一族连续半范数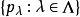 生成。
生成。
定理5设X是Hausdorff的拓扑线性空间,则下列条件等价:
(1)X是可赋范的;
(2)在原点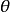 存在有界凸邻域;
存在有界凸邻域;
(3)X是局部凸的且是局部有界的。
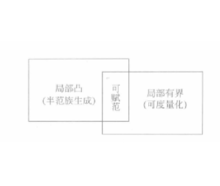
在Hausdorff的拓扑线性空间类中,局部凸空间与局部有界空问是最重要的两类空间,它们间有下述关系(见图1):2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国