闭球套定理(closed ball nest theorem)对度量空间的完备性的一种刻画。 欧氏空间中许多结论均依赖于空间的完备性,如直线上的闭区间套定理,平面内的闭矩形套定理等,在完备的距离空间中,许多与欧氏空间情形类似的结论仍然成立1。
基本介绍定义1 设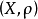 是距离空间,
是距离空间,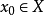 ,
,
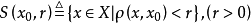 称为以
称为以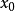 为中心,
为中心, 为半径的开球。
为半径的开球。
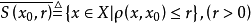 称为以
称为以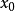 为中心,
为中心, 为半径的闭球。
为半径的闭球。
闭球套定理 设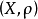 是完备的距离空间,
是完备的距离空间,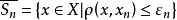 是一列闭球
是一列闭球
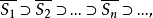 如果球的半径
如果球的半径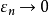 ,则存在唯一的点
,则存在唯一的点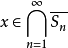 。
。
定理的证明证明: 由命题的条件,不难看到球心组成的序列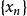 是一个Cauchy列。事实上,对任意n,m,若n≥m,则由
是一个Cauchy列。事实上,对任意n,m,若n≥m,则由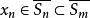 得
得
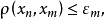 由此立得
由此立得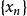 是一个Cauchy列,由X是完备的知存在
是一个Cauchy列,由X是完备的知存在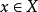 ,使得
,使得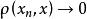 ,在不等式
,在不等式
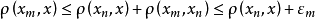 中,固定m并令
中,固定m并令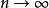 得
得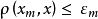 ,这说明
,这说明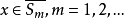 ,故
,故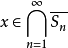 。
。
若另有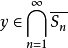 ,且
,且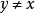 ,则对任意n,有
,则对任意n,有
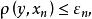 由不等式
由不等式
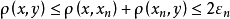 及
及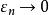 立得
立得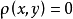 ,从而
,从而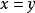 ,这就得到矛盾,所以
,这就得到矛盾,所以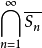 必是单点集。证毕。
必是单点集。证毕。
相关结论在直线上的闭区间套定理中,即使区间的长度不趋于0,所有区间的交仍然是非空的。然而,在一般距离空间中,即使空间是完备的,假如闭球套的半径不趋于0,则其交可能是空集。
从直线上Cauchy准则与闭区间套定理的等价性,人们自然会提出这样的问题:
在距离空间中,闭球套定理与空间的完备性是否等价?
答案是肯定的。事实上,假设在距离空间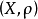 中闭球套定理成立,为证空间的完备性,假设
中闭球套定理成立,为证空间的完备性,假设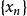 是X中的Cauchy列,于是存在正整数列
是X中的Cauchy列,于是存在正整数列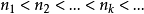 ,使得当
,使得当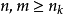 时,
时,
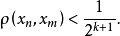 作闭球
作闭球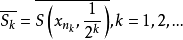 ,则对任意
,则对任意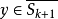 ,由
,由
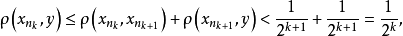 知
知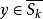 ,故
,故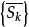 是一个闭球套,于是存在唯一的
是一个闭球套,于是存在唯一的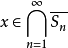 。由
。由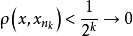 知
知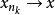 ,又由
,又由
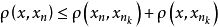 立得
立得 ,即
,即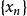 在X中收敛,从而
在X中收敛,从而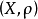 完备1。
完备1。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国