[科普中国]-按度量收敛

按度量收敛是由距离刻画的收敛，度量空间中收敛点列的极限是惟一的。

简介按度量收敛是由距离刻画的收敛。

设(R,p)是度量空间，点列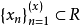，如果存在x0∈R，使当n→∞时，p(xn,x0)→0，就称{xn}按距离ρ收敛于x0，记为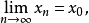或x→x0(n→∞)，并称{xn}为收敛点列，x0为{xn}的极限。

度量空间中收敛点列的极限是惟一的。1

距离设R是一个非空集合，ρ(x，y)是R上的二元函数，满足如下条件：

1.ρ(x,y)≥0且ρ(x,y)=0⇔x=y;

2.ρ(x,y)=ρ(y,x);

3.（三角不等式）ρ(x,y)≤ρ(x,z)+ρ(y,z)，则称ρ(x,y)为两点x，y之间的距离。

度量空间度量空间(Metric Space)，在数学中是指一个集合，并且该集合中的任意元素之间的距离是可定义的，亦称距离空间。一类特殊的拓扑空间。弗雷歇(Fréchet，M.-R.)将欧几里得空间的距离概念抽象化，于1906年定义了度量空间。

在度量空间中，紧性、可数紧性、序列紧性、子集紧性是一致的。可分性、遗传可分性、第二可数性、林德勒夫性是一致的。度量空间必满足第一可数公理，是豪斯多夫空间，完全正规空间，仿紧空间。伪度量空间满足第一可数公理，但一般不是豪斯多夫空间。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学