[科普中国]-序闭包

序闭包(order closure)是序域中实闭包概念在实域上的推广。实域的序闭包总是存在的。此外，一个实域的任何一个序闭包都是毕达哥拉斯域。

概念序闭包(order closure)是序域中实闭包概念在实域上的推广。若F是一个实域，K是F的一个实扩张，则有一个从序空间XK到XF的限制映射rK/F，使得：

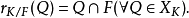实域F的序闭包是F的这样一个实代数扩张L，使得映射rL/F是双射，并且L关于这个性质是极大的；换言之，对于L的任何一个实代数真扩张L′，映射rL′|F不再是双射。实域的序闭包总是存在的。此外，一个实域的任何一个序闭包都是毕达哥拉斯域。1

域代数学的基本概念之一。即具有两个运算的代数系。设F是至少含两个元的集合，在F中定义了两个二元运算：一个称加法，使F成为加群，它的单位元称为F的零元；一个称乘法，使F的非零元构成一个交换群，加法与乘法满足分配律，此时称F为域。例如，全体有理数、全体实数和全体复数在通常的加法与乘法下都构成域，分别称为有理数域、实数域和复数域。域是许多数学分支研究的基础，尤其对代数、代数数论、代数几何等更为重要。

序域序域是一种特殊的域。它是有序结构的域。一个域F，若在它的元素之间存在一个二元关系>，满足下述条件：

1.对于任意a∈F，必有a=0或a>0或-a>0三者之一成立(0指F的零元)；

2.从a>0，b>0可导出a+b>0及ab>0；

则称>是F的一个序，带有序>的域F称为序域，记以(F，>)。凡是能在其中规定序的域，就称为可序的，或称可序域。在实数域R和有理数域Q中，通常的大小关系就给出它们的一个序。因此R和Q都是可序域，而且，它们只能有这样给出的序。不过，并非所有的可序域都只有惟一的序。

闭包闭包是图论的一个基本概念。指由一个图所派生出的另一个图。具体地说，一个图G的闭包H是指符合下列条件包含边最少的图：G是H的支撑子图；对于H上任何两不相邻节点v和w，都有ρH(v)+ρH(w)