同伦论
同伦论是拓扑学的重要概念。1
直观地说,从拓扑空间X到拓扑空间y的连续映射f,g是同伦的,是指在y中可将f 连续形变成 g,设都是连续映射,若存在连续映射,使得对所有,则称f和g是同伦的映射,记为称H 为从f到g的一个同伦或伦移,这时的,若对所有t,同伦都是X到Y的同胚,则称f合痕于g。应该指出,映射的同伦关系是从拓扑空间X到Y的所有连续映射所成集合c(x,y)上的一个 等价关系,它将这些映射分成一些等价类,称每个等价类为一个同伦类。研究映射的同伦分类问题是同伦论的基本内容之一。
直观地说,从拓扑空间X到拓扑空间y的连续映射f,g是同伦的,是指在y中可将f 连续形变成 g,设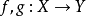 都是连续映射,
都是连续映射,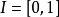 ,若存在连续映射:
,若存在连续映射: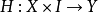 ,使得对所有
,使得对所有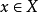 ,
,
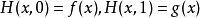 则称f和g是同伦的映射,记为:
则称f和g是同伦的映射,记为: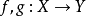 ,称H 为从f到g的一个同伦或伦移,这时的
,称H 为从f到g的一个同伦或伦移,这时的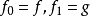 ,若对所有t,同伦f1都是X到Y的同胚,则称f合痕于g。应该指出,映射的同伦关系是从拓扑空间X到Y的所有连续映射所成集合c(x,y)上的一个 等价关系,它将这些映射分成一些等价类,称每个等价类为一个同伦类。研究映射的同伦分类问题是同伦论的基本内容之一。2
,若对所有t,同伦f1都是X到Y的同胚,则称f合痕于g。应该指出,映射的同伦关系是从拓扑空间X到Y的所有连续映射所成集合c(x,y)上的一个 等价关系,它将这些映射分成一些等价类,称每个等价类为一个同伦类。研究映射的同伦分类问题是同伦论的基本内容之一。2
详细概念覆叠空间亦称覆盖空间。同伦论中一个重要概念。设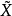 是道路连通空间,X是连通且局部道路连通空间,p:
是道路连通空间,X是连通且局部道路连通空间,p: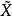 →X是连续满映射,若对于X中每一点x都有一个道路连通开邻域U,使得对于
→X是连续满映射,若对于X中每一点x都有一个道路连通开邻域U,使得对于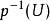 的每个连通分支V,p在V上的限制p|V:V→U是同胚,则称(
的每个连通分支V,p在V上的限制p|V:V→U是同胚,则称(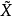 ,p)为X的覆叠空间,称p为覆叠映射,称X为底空间,这样的邻域U称为x的可允许的邻域。例如,指数映射π:R^1→S^1,把t∈R^1映为e∈S^1,则(R^1,π)是S^1的覆叠空间。若对于1∈S,取:
,p)为X的覆叠空间,称p为覆叠映射,称X为底空间,这样的邻域U称为x的可允许的邻域。例如,指数映射π:R^1→S^1,把t∈R^1映为e∈S^1,则(R^1,π)是S^1的覆叠空间。若对于1∈S,取:
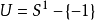
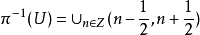
则:
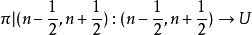 为同胚。
为同胚。
覆叠空间理论包括映射提升定理,覆叠空间的分类定理,以及万有覆叠空间的存在性等内容。例如道路提升定理:设(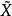 ,p)是X的覆叠空间,p:
,p)是X的覆叠空间,p: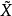 →X为覆叠映射,若a∈X,b∈p(a),v为X的以a为起点的道路,则
→X为覆叠映射,若a∈X,b∈p(a),v为X的以a为起点的道路,则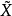 内有惟一的以b点为起点的道路
内有惟一的以b点为起点的道路 ,满足p°
,满足p°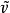 =v,
=v,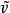 称为道路v的提升。类似地,有闭路同伦提升定理:设(
称为道路v的提升。类似地,有闭路同伦提升定理:设(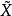 ,p)是X的覆叠空间,若F:I×I→X为连续映射,满足条件:
,p)是X的覆叠空间,若F:I×I→X为连续映射,满足条件:
F(0,t)=F(1,t)=a, 0≤t≤1,b∈p(a),
则存在惟一的连续映射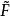 :I×I→
:I×I→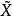 满足条件:
满足条件:
p°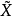 =F,
=F, 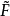 (0,t)=
(0,t)=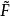 (1,t)=b, 0≤t≤1,
(1,t)=b, 0≤t≤1,
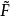 称为F的提升。根据上述提升定理可知:覆叠映射p的诱导同态p*: π1(
称为F的提升。根据上述提升定理可知:覆叠映射p的诱导同态p*: π1(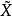 ,b)→π1(X,a)是单同态。
,b)→π1(X,a)是单同态。
道路连通空间道路连通空间一类拓扑空间。若对于拓扑空间X中的任意两点都存在以这两点分别为始点与终点的道路,则称X为道路连通空间。若拓扑空间的子集作为子空间是道路连通的,则称它为道路连通子集。道路连通空间一定是连通空间,但是,其逆不成立。例如,X为{(x,y)|y=sin(1/x),x≠0}与{(0,y)|y∈[-1,1]}的并集且赋予通常拓扑,则X是连通空间但不是道路连通空间。3
映射提升定理关于覆叠空间的一条定理。设(X~,p)是X的覆叠空间,对于连续映射f:Y→X,若存在连续映射f~:Y→X~,满足条件p°f~=f,则称f~为f的提升。映射提升定理:若Y是连通且局部道路连通空间,r∈Y,(X~,p)是X的覆叠空间,a∈X,b∈p(a),则连续映射f:(Y,r)→(X,a)存在提升f~:(Y,r)→(X~,b)的充分必要条件为f*(π1(Y,r))p*(π1(X~,b)),并且当提升f~存在时它是惟一的。这里f*和p*分别为连续映射f和覆叠映射p对应的基本群之间的诱导同态。4




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国