[科普中国]-映射提升定理

概念

映射提升定理(map lifting theorem)是关于覆叠空间的一条定理。设(X'，p)是X的覆叠空间，对于连续映射f：Y→X，若存在连续映射f'：Y→X'，满足条件p°f'=f，则称f'为f的提升。映射提升定理：若Y是连通且局部道路连通空间，r∈Y，(X'，p)是X的覆叠空间，a∈X，b∈p(a)，则连续映射：

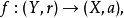存在提升：

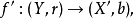的充分必要条件为：

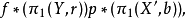并且当提升f'存在时它是惟一的。这里f*和p*分别为连续映射f和覆叠映射p对应的基本群之间的诱导同态。1

覆叠空间覆叠空间(covering space)亦称覆盖空间，同伦论中一个重要概念。

覆盖空间在同伦理论，谐波分析，黎曼几何和差分拓扑中起着重要作用。例如，在黎曼几何中，分支是覆盖地图概念的概括。覆盖空间也与同伦群体研究，特别是基础群体的研究深深交织在一起。一个重要的应用来自结果，如果X是一个“足够好”的拓扑空间，则X的连接覆盖的所有同构类的集合与X的基本组的子群的共轭类之间存在着双重的差异。

覆叠空间理论包括映射提升定理，覆叠空间的分类定理，以及万有覆叠空间的存在性等内容。2

连续映射连续映射(continuous mapping)拓扑空间之间的一类重要映射。

设X，Y为任意两个集合，映射f：X→Y，对于x0∈X，有y0=f(x0)，如果对于y0的任意邻域U(y0)，总能找到x0的邻域U(x0)，使得：

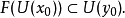则称映射f在点x0是连续的。如果映射f在集合X的每一点都是连续的，则称映射f为X上的连续映射。

高等数学中连续函数的定义与这里的连续映射概念是一致的。

设(X,T)与(Y,Τ)是两个拓扑空间，f:X→Y是映射，x∈X。若f(x)的每一邻域关于f的原像是x的邻域，则称f在点x处是连续的。若f在X的任意点是连续的，则称f是(X,T)到(Y,U)的连续映射。f为连续映射的等价条件有很多，例如：

1.Y的每一开集的原像是X的开集；

2.Y的每一闭集的原像是X的闭集；

3.对于任意x∈X和f(x)的任意邻域U，存在x的邻域V使得f(V)⊂U；

4.对于X的每一子集A，有：

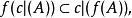
5.对于Y的每一子集B，有：

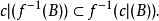
道路连通空间一类拓扑空间。若对于拓扑空间X中的任意两点都存在以这两点分别为始点与终点的道路，则称X为道路连通空间.若拓扑空间的子集作为子空间是道路连通的，则称它为道路连通子集。道路连通空间一定是连通空间，但是，其逆不成立。例如，X为{(x，y)|y=sin(1/x)，x≠0}与{(0，y)|y∈[-1，1]}的并集且赋予通常拓扑，则X是连通空间但不是道路连通空间。

同伦论代数拓扑学中研究与连续映射的连续形变有关的各种课题，是代数拓扑学的一个主要组成部分。同伦概念的直观解释就是连续变形，以此为基础定义的基本群被称为同伦群。最早论及同伦群的是法国数学家庞加莱，他于1895年引进的复形基本群被称为第一同伦群。1912年荷兰数学家布劳威尔引入同维流形之间映射的度以研究同伦分类，开创不动点理论。20世纪20年代德国数学家霍普夫探讨了球面同伦理论。20世纪30年代波兰数学家胡雷维奇建立了群的同伦理论，引进拓扑空间的n维同伦群。另一位波兰数学家博苏克于1936年定义了从拓扑空间到n维球面的映射类的和，由此得到博苏克上同伦群。20世纪40年代原苏联数学家庞特里亚金给出从(n+k)维球到n维球的映射同伦分类，被称为庞特里亚金类。20世纪50年代初，法国数学家塞尔提出了研究同伦群的新方法，利用纤维化的谱序列，取得了球面同伦群计算的突破性进展。20世纪50年代末英国数学家J.F.亚当斯提出新的谱序列，成为研究同伦论的重要工具。20世纪60年代初广义同调论的发展使同调的问题可以转化为同伦的问题，从此代数拓扑学的这两个主要分支统一起来，共同获得重大发展。 3