定义
对于两个集合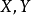 ,如果按照一个对应关系(规则),使得对于
,如果按照一个对应关系(规则),使得对于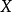 中的每一元素
中的每一元素 ,都有
,都有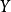 中的一个(几个)确定的元素
中的一个(几个)确定的元素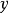 与之对应,那么我们把这个对应关系叫做集合
与之对应,那么我们把这个对应关系叫做集合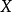 到集合
到集合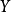 的单值(多值)映射,多值映射也称“集值映射”。通常用
的单值(多值)映射,多值映射也称“集值映射”。通常用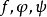 …等符号来代表映射,当
…等符号来代表映射,当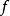 表示一个由集合
表示一个由集合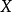 到集合
到集合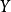 的映射,那么记
的映射,那么记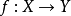 ,或
,或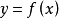 ,对任意
,对任意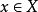 ,对于任意集合
,对于任意集合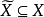 ,我们把集合
,我们把集合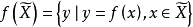 叫做
叫做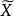 的象,而对任何集合
的象,而对任何集合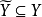 ,我们把集合
,我们把集合 叫做
叫做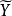 的原象(逆象)。2
的原象(逆象)。2
相关概念凹函数定义1 对凸集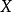 上的函数
上的函数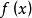 ,如果不等式
,如果不等式
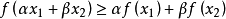 对任意的
对任意的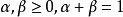 和任意
和任意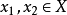 成立,那么我们称函数
成立,那么我们称函数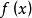 为
为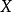 上的凹函数。当不等式是严格不等式时,我们叫
上的凹函数。当不等式是严格不等式时,我们叫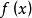 为严格凹函数。2
为严格凹函数。2
类似可定义凸函数。凹函数图像如图1。
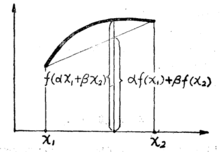
下面的定义都将限制集合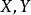 是
是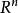 中的有界闭、凸集。
中的有界闭、凸集。
上半连续定义2 对多值映射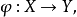 序列
序列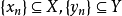 ,如果当
,如果当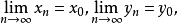 且
且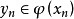 时有
时有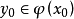 ,那么,我们说映射
,那么,我们说映射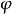 是上半连续的。
是上半连续的。
当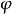 为单值映射时,以上就是它的连续性定义。
为单值映射时,以上就是它的连续性定义。
下半连续定义3 若从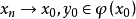 能够推出存在
能够推出存在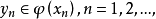 使得
使得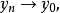 则称映射
则称映射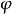 为下半连****续。
为下半连****续。
由定义得知,要证明映射的下半连续性,就要找出满足定义条件的序列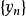 来。
来。
线性组合关于多值映射的线性组合,我们有如下定义。
定义4 假定有几个映射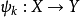 是上半连续的,
是上半连续的, 是凸且有界闭的集合,那么映射
是凸且有界闭的集合,那么映射
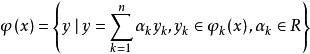 叫做映射
叫做映射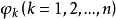 的线性组合,并用记号
的线性组合,并用记号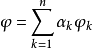 。2
。2
相关定理定理1假定集合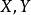 是凸,有界闭集,定必在
是凸,有界闭集,定必在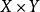 上的连续函数
上的连续函数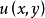 关于
关于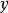 是凹的,那么映射
是凹的,那么映射
 是上半连续的,且集合
是上半连续的,且集合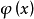 是非空凸、闭集。2
是非空凸、闭集。2
定理2假定集合X与Y是凸、有界闭集,函数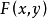 定义在
定义在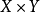 上,且对x与y分别是连续的,对y是凸的,如果存在
上,且对x与y分别是连续的,对y是凸的,如果存在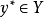 ,使得对所有
,使得对所有 满足
满足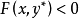 。那么映射
。那么映射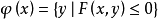 既是上半连续又是下半连续,并且集合
既是上半连续又是下半连续,并且集合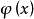 是非空,凸且闭的。
是非空,凸且闭的。
定理3假定连续函数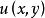 定义在
定义在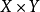 上,其中
上,其中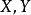 是凸,有界闭集,
是凸,有界闭集,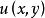 对y是凹的,并且多值映射
对y是凹的,并且多值映射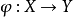 是上半且下半连续的,集
是上半且下半连续的,集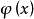 非空,对任意
非空,对任意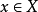 是凸的。那么映射
是凸的。那么映射
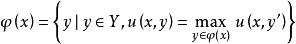 是上半连续的,集合
是上半连续的,集合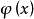 是非空,凸且有界闭的集合。2
是非空,凸且有界闭的集合。2
定理4关于多值映射的线性组合,有如下结论。
上半连续映射的线性组合也是上半连续的。
定理5下述的日本学者卡库坦的多值映射不动点定理,在经济数学中占有重要地位。
假定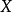 是凸且有界闭的
是凸且有界闭的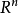 中的子集,映射
中的子集,映射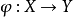 是上半连续的,集合
是上半连续的,集合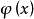 是非空凸集,那么存在
是非空凸集,那么存在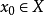 ,使
,使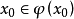 。2
。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国