[科普中国]-多项式不可分次数

多项式不可分次数是刻画不可分多项式与相应可分多项式次数差异的一个数。

简介多项式不可分次数是刻画不可分多项式与相应可分多项式次数差异的一个数。

若 f(x) 是特征为 p>0 的域 F上首 1 不可分的既约多项式，则必存在一个可分的不可约多项式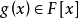 和非负整数 e，

此时称 pe 为 f(x) 的不可分次数，e 称为 f(x) 的不可分指数，g(x) 的次数称为 f(x) 的约化次数，若约化次数为m，则 f(x) 在某个代数闭包内恰有 m 个不同的根，且每个根的重数为 pe，有等式：deg f(x)=约化次数 pe。

当 f(x) 的次数与其不可分次数相等，即约化次数为1时，称f(x)为纯不可分多项式，这时 f(x) 具有形式

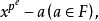
它在代数闭包内的根完全相同。1

纯不可分元(purely inseparable element)

代数扩域中的一种特殊元。设域 F 的特征 p>0，K/F 是代数扩张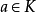， 称为 F 上的纯不可分元是指 α 在 F 上的最小多项式为纯不可分多项式；它等价于存在整数 e≥ 0，使得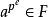. 具有这种性质的最小整数 e，称为 α 的纯不可分指数。

对于代数扩张 K/F，K 中所有在 F 上为纯不可分指数，对于代数扩张 K/F ， K 中所有在 F 上为纯不可分元的元素全体是 K 的一个包含 F 的子域，这个子域称为 F 在 K 中的纯不可分闭包。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学