[科普中国]-诱导拓扑

拓扑性质

设X是一个非空集合，X的幂集的子集（即是X的某些子集组成的集族）T称为X的一个拓扑。当且仅当：

1．X和空集{}都属于T；

2．T中任意多个成员的并集仍在T中；

3．T中有限多个成员的交集仍在T中。

称集合X连同它的拓扑τ为一个拓扑空间，记作（X,T）。

称T中的成员为这个拓扑空间的开集。

定义中的三个条件称为拓扑公理。（条件（3）可以等价的换为τ中两个成员的交集仍在τ中。）

从定义上看，给出某集合的一个拓扑就是规定它的哪些子集是开集。这些规定不是任意的，必须满足三条拓扑公理。

一般说来，一个集合上可以规定许多不相同的拓扑，因此说到一个拓扑空间时，要同时指明集合及所规定的拓扑。在不引起误解的情况下，也常用集合来代指一个拓扑空间，如拓扑空间X，拓扑空间Y等。

同时，在拓扑范畴中，我们讨论连续映射。定义为：f: (X,T1) ------> (Y,T2) （T1,T2是上述定义的拓扑）是连续的当且仅当开集的原像是开集。两个拓扑空间同胚当且仅当存在一一对应的互逆的连续映射。同时，映射同伦和空间同伦等价也是很有用的定义。2

诱导拓扑定义诱导拓扑(induced topology)是指构造拓扑的一种方法。设f.是集合X到拓扑空间(Y , U)的映射。在X上的所有使得f连续的拓扑中，最粗的拓扑T称为由(Y,U)及f确定的诱导拓扑。实际上，

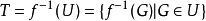反之，若f是拓扑空间(X,T)到集合Y上的映射。在Y上的所有使得f连续的拓扑中，最细的拓扑U称为由(X,T)及f确定的诱导拓扑。也称为由f与X上的拓扑确定的Y的商拓扑。实际上，3

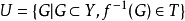
拓扑空间的性质性质1集合X的离散拓扑T是X的最大拓扑，即对X的每一个拓扑T1，均有。

证明由拓扑T1的定义可得： 对A∈T1，有A∈ P(x)。此外，T是X的离散拓扑意味着T =P(x) ，因此，A∈T，从而由A的任意性可知。

性质2离散拓扑空间(X，T) 中：

①点x的邻域系是Ux= AX | x∈ A}，即凡是X的包含x的子集都是x的邻域。

② X的每一个子集既开又闭。

证明对任意的x∈X，有{x}∈P(x)= T，故{x} 是开集。另外，对任意的x ∈ AX，有x∈{x}A，从而由邻域的定义可知A是X的邻域。

设A是X中的任一子集，那么有A∈P(x)=T，即A是开集。另一方面，由X ～ AX可得Ac∈P(x)= T， 故A是闭集。

注： 一般拓扑空间的子集也可能是既不开也不闭的。

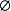性质3离散拓扑空间(X，T) 中，若AX，则A的导集A' = ，即A中不含有任何一个聚点。

证明 对任意的x∈X，存在x的一个开邻域{x} ，使得{x}∩(A －{x} )=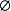 ，从而x不是A的聚点，因此，由x的任意性可得：集合A中不含有任何一个聚点，即A' =。4