[科普中国]-剩余类次数

剩余类次数是素除子或素理想的剩余类域的扩张次数，也称为相应赋值素理想的次数或剩余类次数。

简介剩余类次数是素除子或素理想的剩余类域的扩张次数。

若域 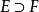是 E 的非阿基米德素除子， P 是 Q 在 F 的限制（或称 Q 是 P 的延拓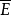），和 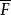是 E 在 Q 和 F 在 P 的剩余类域，则域扩张次数 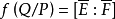称为 Q 在 P 上的次数，或 E/F 在 Q 的剩余类次数。也称为相应赋值素理想的次数或剩余类次数。1

素除子(prime divisor)

素除子是一个赋值等价类。两个赋值等价当且仅当其决定的拓扑相同，也当且仅当其中一个赋值是另一赋值的幂，由此得到的赋值等价类称为素除子。

素理想素理想一词最早可追溯到费马最后的定理（也称费马大定理） 的研究， 即证明著名的费马方程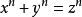，当n>2时没有非零整数解。这一问题的研究首先被扩展到n次单位根扩域上--分圆域--来讨论。 人们试图利用类似整数的算术基本定理来证明方程无解，但遗憾的是, 分圆域上算术基本定理不一定成立。 为了弥补这一缺陷，库莫引入了理想数的概念--即“理想”的雏形。

一个环R中的理想P如果满足以下条件就称作素理想：P是R的真理想，且 对任何a，b∈R, 如果乘积ab ∈P，那么a或b中至少有一个属于P。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学