[科普中国]-一致覆盖

概念

一致覆盖(uniform cover)是一致空间X上的一类特殊的覆盖。设U是X上的一致结构。对于每一U∈U，若：

C(U)={U(x)|x∈X}，1

其中U(x)={y|(x，y)∈U}，则C(U)是X的一个覆盖。X上的覆盖C称为关于U的一致覆盖，若C是某一C(U)的加细，其中U∈U。若S是X上的一致覆盖族，S诱导的X上的一致结构为U，则S中的元恰好是关于U的所有一致覆盖。

一致结构一致结构是集合上的一种结构。设X为集合，U为X×X的非空子集族。若U满足下列条件，则称U是X上的一致结构：

1.U的每一个元包含对角线Δ.

2.若U∈U，则U∈U，其中

U={(x，y)|(y，x)∈U}.

3.若U∈U，则存在V∈U使得V°VU，其中

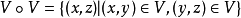
4.若U，V∈U，则U∩V∈U.

5.若U∈U并且UVX×X，则V∈U.

具有一致结构U的集合X称为一致空间，记为(X，U)。一致空间的概念是韦伊(Weil，A.)于1938年引入的。布尔巴基(Bourbaki，N.)于1940年首先给予系统的论述。图基(Tukey，J.W.)于1940年用覆盖族定义并研究了一致空间的等价的概念。艾斯贝尔(Isbell，J.R.)于1964年出版的书中，包含了用覆盖叙述的一致空间理论的重要发展。一致空间也可用伪度量族来描述，它是由布尔巴基于1948年给出的。2

覆盖覆盖是数学的一个重要概念。这里指一类节点子集。具体地说，图的一个节点子集使该图的每一条边都与这个子集中一个节点关联，称这样的节点子集为覆盖集，也称点覆盖集，简称覆盖。图G的最小覆盖，也称最小点覆盖，是指在图的所有覆盖中，节点数最少的覆盖。G的最小覆盖的节点数称为G的覆盖数，或点覆盖数，常记为β(G)。一个图称为覆盖临界图，或点覆盖临界图，若从这图上去掉任何一条边后，所得的图的覆盖数都小于原图的覆盖数。设有一个最小覆盖M，若对于它的任何一个子集M′，与M′中节点相邻的不在M中的节点的数目总不比M′的节点数少，则称M为一个外部最小覆盖或外最小点覆盖。不是任何一图都有外最小覆盖。事实上，一个图有外最小覆盖当且仅当它有一个点核，或边核。

拓扑空间的基本概念。一种特殊的集族。设A是由集合组成的族.若它的所有成员的并包含集合B，则称该集族A是B的一个覆盖，或称A覆盖B.在拓扑空间X中，若A的每一成员都是X的开集(或闭集)，并且A覆盖X，则称A是X的开覆盖(或闭覆盖)。若A的子族A1也是B的覆盖，则称A1是A的子覆盖。当覆盖A为有限集或可数集时分别称A为有限覆盖或可数覆盖。

一致覆盖族一致覆盖族是一类特殊的覆盖族。设S={Uα}是集合X的覆盖族.称S为X上的一致覆盖族，若S满足下列条件：

1.对于X的任意覆盖U，若存在Uα∈S，使得Uα是U的加细，则U∈S。

2.对于任意Uα，Uβ∈S，存在Uγ∈S使得Uγ是Uα与Uβ的共同加细。

3.对于任意Uα∈S，存在Uβ∈S，使得Uβ是Uα的星加细。

当X的覆盖族S满足条件3时，称S为一致覆盖族的子基。又当S满足条件2与3时，称S为一致覆盖族的基.设S为X上的一致覆盖族，对于任意x∈X，若把

{Uα(x)|Uα∈S}

确定为x的邻域系，则在X上可诱导出拓扑，称此拓扑为由S诱导的X上的拓扑。由X上的一致覆盖族S可惟一确定X上某个一致结构U，使得由S诱导的X上的拓扑恰好是由U诱导的X上的一致拓扑。上述U的基是所有形如

∪{A×A|A∈A}

的集族，其中A是S中的元。3

一致拓扑一致拓扑是指由一致结构诱导的拓扑。设(X，U)为一致空间，T是X的子集，满足：对于任意x∈T，存在U∈U使得U(x)T，其中U(x)={y|(x，y)∈U}.所有这种T组成的集族T是X上的一个拓扑，称为由一致结构U诱导的拓扑或一致拓扑。当由一致结构U诱导的拓扑空间X为紧空间时，则和X的拓扑一致的一致结构是惟一确定的。一致空间是完全正则的，并且完全正则空间具有和它的拓扑一致的一致拓扑。即有下述结果：集合X上的拓扑T为X上的某个一致结构的一致拓扑的充分必要条件是，(X，T)为完全正则空间。