[科普中国]-第一类型集

第一类型集(first category set)是拓扑空间的一类特殊的点集。若拓扑空间X的子集A可表为可数个无处稠密集的并，则称A为X的第一类型集。若A不是第一类型集，则称A为第二类型集。在实数空间中，有理数全体是第一类型集，无理数全体是第二类型集，它们都是实数空间中稠密的边缘集。可数个第一类型集的并仍为第一类型集，有人亦称第一(二)类型集为第一(二)范畴集1。

基本介绍稀疏集 设X为一距离空间，A是X的子集。如果A在X的任何一个非空开集中均不稠密，则称A为稀疏集。

定义中的非空开集可以换成非空开球，下面的定理给出稀疏集的一个特征。

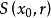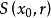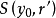定理1 距离空间X的子集A为稀疏集的充分必要条件是对任一开球，存在另一个含于中的开球使

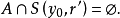
定义 设A为距离空间X的子集，如果A可以表示成至多可列个稀疏集的并，则称A是第一类型集，又称“第一纲集”，凡不是第一类型的集均称为第二类型集，又称“第二纲集”。

因此，距离空间X的子集或者是第一类型的集或者是第二类型的集，二者必居其一。

有限个或可数个第一类型集的和是第一类型的集2。

例题分析例1（1）n维Euclid空间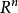中的任一有限子集是稀疏集，特别地，任一单元素集是稀疏集，因此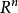中的任一可列集是第一类型的集。

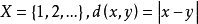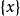（2）设，因为，故在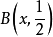中稠密，于是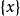不是稀疏集。因此，包含在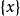中的任一稀疏集必为空集。如果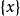是可数个稀疏集的并，则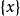必为空集，这样就产生了矛盾。因此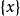，为第二纲集。

第一类型的集与第二类型的集都是相对于一定的距离空间而言的，因而也都与事先给定的空间有着不可分割的联系2。

相关定理定理2设X是完备的距离空间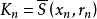，是X中的一列闭球，满足

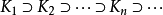(称为闭集套).

如果，则有唯一的点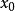含于所有球中。

定理2的逆命题也成立。

定理3 如果距离空间X中的任一半径趋于零的闭球套都有非空的交，则空间X是完备的。

下面的定理给出了完备距离空间的一个重要特性。

定理4(贝尔(Baire))完备的距离空间是第二类型的集2。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学