[科普中国]-射影极小曲面

射影极小曲面(projective minimal surface)是射影曲面论的基本元素之一。这个定义是汤姆森(Thomson，G.)于1928年给出的。射影极小曲面有许多特征。

概念射影极小曲面(projective minimal surface)是射影曲面论的基本元素之一。变分问题：

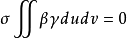的解曲面。这个定义是汤姆森(Thomson，G.)于1928年给出的。射影极小曲面有许多特征，例如：

1.射影极小曲面的射影极小曲线(曲面关于伴随二次曲线K2的非欧线素ds2=0给出的两族曲线)构成共轭网。

2.射影极小曲面的切平面关于对应的伴随二次曲面的极在对应的李二次曲面上。

3.射影极小曲面的德穆林变换是可逆的。

射影微分射影微分几何学(projective differential geometry)从属于射影变换群。其思想来源于C.F.克莱因1872年的著名演说“埃朗根纲领”，在那里将几何学归结为可逆变换群的几何不变量理论加以分类。研究的对象主要是曲线、曲面、共轭网等在射影变换群下的不变量、协变图形及其性质。

射影微分几何是从属于射影变换群的微分几何，在达布的著名的曲面论中已含有它的萌芽，它主要是在20世纪初期按照克莱因的思想展开的，到20世纪40年代趋于完善。主要研究对象是曲线、曲面和共轭网等在射影变换群下的不变量、协变图形及其性质。1

射影微分几何的研究方法大致有下列三种：

第一种是以富比尼(G.Fubini)为首的意大利学派的方法。以曲面论为例，设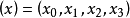是三维射影空间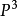中齐次坐标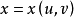，是曲面S的参数表示，用一种射影不变的方法确定的比例因子，得到富比尼规范坐标，构造二次和三次形式：

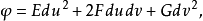
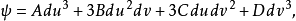式中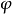和普通曲面论中第二基本形式只相差一个因子，于是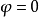定义了曲面的两族渐近曲线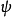，和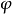满足配极关系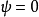，定义曲面的三族达布曲线，这两个基本形式的系数满足一系列关系式，即曲面的基本方程，同普通曲面论一样，可导出射影曲面论的基本定理。

第二种是嘉当(E.Cartan)的活动标架法。嘉当用活动标架法重建射影曲面论，问题归结为普法夫方程组，可积条件即嘉当结构方程，从而导出许多结果，近年来，用嘉当方法发展起来高维射影空间共轭网理论。

第三种是以苏步青为首的中国学者开创和发展的结构式射影微分几何方法，主要是用几何作图法来建立射影协变的构图和不变量。例如用平面曲线在其某种奇点的不变量来表达其他的几何不变量。

共轭网共轭网是射影曲面论的重要概念之一。n维射影空间Pn中曲面上一种曲线网，在其中一族的每条固定曲线上各点做另一族各曲线的切线构成一个可展曲面。曲面x=x(u，v)具有共轭网(u，v)的充分必要条件是x满足拉普拉斯方程：

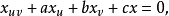其中a，b，c是u，v的函数。

李二次曲面李二次曲面是射影曲面论中重要元素之一。一种射影协变的二次曲面。设Γ和Γ-是曲面S上交于正常点O的两条渐近曲线，Γ和Γ-的渐近直纹面都有一个是切线曲面。李(Lie，S.)证明：Γ的另一渐近直纹面沿Γ-的切线的密切二次曲面(Γ在O的渐近密切二次曲面)和Γ-的另一渐近直纹面沿Γ的切线的密切二次曲面(Γ-在O的渐近密切二次曲面)重合。这个二次曲面称为李二次曲面。

德穆林四边形德穆林四边形是一种射影协变四边形。德穆林(Demoulin，A.)于1908年研究李二次曲面时得到。当点M在曲面S上变动时，相应的李二次曲面有∞2个，八个包络面中有四个与S重合，其余四个与M点的李二次曲面切于另外四点.这四点形成的四面体称为曲面S在M的德穆林四面体，这四点对应的四条直线是李二次曲面的母线，构成的空间四边形称为德穆林四边形。点M变动时，四点的轨迹称为S的德穆林变换。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学