[科普中国]-拟弗罗贝尼乌斯环

简介

拟弗罗贝尼乌斯环简称QF环，是具有对偶性质的重要环类。

若幺环R作为左（右）R模是内射R模，则称R为左（右）自内射环（self-injective ring）。

若幺环R为左诺特左自内射环，等价地，R既是左右阿廷的又是左右自内射的，则称其为拟弗罗贝尼乌斯环。

若拟弗罗贝尼乌斯环R作为左（或右）R模都有 ，则称其为弗罗贝尼乌斯环（Frobenius ring ）。1

费丝-沃克定理[Faith-Walker theorem]：幺环R为拟弗罗贝尼乌斯环当且仅当每个投射左R模都是内射的，当且仅当每个内射左R模都是投射的。

性质QF环的一个重要同调性质是：R是QF环当且仅当任意IZ投射模是内射的，且任意内射R模是投射的。

若有限维幺K代数A满足：A与作为左A模同构，则称A为弗罗贝尼乌斯代数（Frobenius algebra）。若K为域，G为有限群，则群代数KG为弗罗贝尼乌斯代数。有限维K代数A是弗罗贝尼乌斯代数当且仅当存在线性映射 使得Ker𝑓不包含非零的左或右理想时成立。

若有限维幺K代数A满足：A与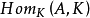 的不可分解直和项在不记同构和项数的意义下对应相同，则称A为拟弗罗贝尼乌斯代数（quasi-Frobenius algebra）。设A是有限维K代数。则A是（拟）弗罗贝尼乌斯代数当且仅当A是（拟）弗罗贝尼乌斯环时成立。

发展拟弗罗贝尼乌斯环是中山正(Nakayama , T.)于1939年引入的，它是左右对称的且是左和右阿廷的。

阿尔门翠尼(Ar-mendriaz , E. P.)于1980年把诺特条件减弱为本质左(或右)理想满足降链条件。

胡恩(Huynh , D.)和韦斯宝尔(Wisbauer,R.)于1989年进一步把上述降链条件减弱为升链条件。