[科普中国]-绝对全曲率

绝对全曲率是表征曲面整体性质的一个重要内蕴概念。绝对全曲率的概念已被陈省身、拉肖夫(Lashof,R.K.)等推广到高维子流形上。

简介绝对全曲率是表征曲面整体性质的一个重要内蕴概念。

设 S 是 R3中的紧致连通闭曲面，K 是它的高斯曲率，积分

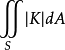
称为曲面 S 的绝对全曲率，这里 dA 是曲面 S 的面积元素。

曲面的绝对全曲率曲面的绝对全曲率满足不等式

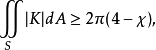这里 χ 是曲面欧拉一庞加莱示性数，式中等号当且仅当 S 是卵形面时成立。

绝对全曲率的概念已被陈省身、拉肖夫(Lashof,R.K.)等推广到高维子流形上。1

全平均曲率(total mean curvature)

全平均曲率是表征曲面整体性质的一个重要外在概念。

设 S 是 R3 中的紧致连通闭曲面，它的平均曲率为 H ，积分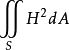称为曲面S的全平均曲率，这里 dA 是曲面 S 的面积元素。

它是由威尔莫(Willmore,T. J.)于1965年首先提出的。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学