[科普中国]-本原环

概念

本原环(primitive ring)是一类重要的环。研究雅各布森根时引入的，其后被广泛讨论与应用。若环R有一个忠实右(左)R单模(即忠实既约右(左)R模)，则称R为右(左)本原环。通常将右本原环简称本原环。一般说来，左本原环未必是本原环，但当R有极小单侧理想时，左本原性与本原性一致。任何本原环皆为素环。雅各布森(Jacobson，N.)引入本原环来代替有限条件下的单环，从而得出在没有有限条件限制下的一般半单环的结构定理，这是环论的重大发展。1

环论环论是抽象代数学的主要分支之一。它是具有两个运算的代数系。在非空集合R中定义加法“+”和乘法“·”运算，使得R中任意元a，b，c适合条件：

1.R对加法为交换群，称为R的加法群，记为(R，+)；

2.R对乘法适合结合律，即(R，·)是半群，称为R的乘法半群；

3.乘法对加法的左、右分配律成立，即：

a·(b+c)=a·b+a·c (左分配律)，

(b+c)·a=b·a+c·a (右分配律)；

则称R为结合环，简称环(通常a·b写为ab)。它是环论研究的主要对象。环论起源于19世纪关于实数域的扩张与分类，以及戴德金(Dedekind，J.W.R.)、哈密顿(Hamilton，W.R.)等人对超复数系的建立和研究。韦德伯恩(Wedderburn，J.H.M.)于1907年给出的结构定理给出代数研究的模式，也成为环结构研究的模式。20世纪20-30年代，诺特(Noether，E.)建立了环的理想理论，阿廷(Artin，E.)又将代数结构定理推广到有极小条件的环。同时，对非极小条件的环，冯·诺伊曼(von Nenmann，H.)建立了正则环理论，相继盖尔范德(Гельфанд，И.М.)创立了赋值环，克鲁尔(Krull，W.)建立了局部环理论，以及哥尔迪(Goldie，A.W.)完善了极大条件环理论。

20世纪40年代，根论迅速发展，尤其是雅各布森(Jacobson，N.)于1945年引入的被称为雅各布森根的概念后，建立了本原环理论、半本原环的结构定理与本原环的稠密性定理，完善和深化了不带附加条件环的理论。20世纪50年代中期，阿密苏(Amitsur，S.A.)、库洛什(Kurosh，A.)创立了根的一般理论，环论已趋完善。

另一方面，由群表示研究的影响，产生模、群环与分次环的理论。20世纪20年代初，诺特引入了模的概念，并研究模对有限群表示的作用与环结构之间的关系，用模的语言去刻画环，特别是20世纪50年代以后，同调代数的迅速发展，使环的理论进入更高层次虽然，早在1854年，凯莱(Cayley，A.)就引入了群代数，然而，它的研究是从20世纪30年代开始直到60—70年代，受群表示论与环的理论的推动才蓬勃发展起来的。20世纪70年代后，由于分次代数的推动，群代数进入新的阶段——交叉积的研究.分次环与模发展的另一动力是交换代数几何中射影代数簇，20世纪70年代以来，由于非交换代数几何及群表示论的推动，环论已进入一个新的阶段。

环环是对并与差运算封闭的集类，测度论中重要概念之一。设F是Ω上的一个非空集类。如果它对集的并及差运算封闭，即对任何A，B∈F，都有A∪B∈F，A\B∈F，则称F为Ω上的环。例如，若F是由实直线R上任意有限个左开右闭的有限区间的并集：

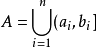
的全体构成的集类，则F是R上的一个环。环也是对于交与对称差运算封闭的集类，并按这两种运算成为布尔环。要把R上的勒贝格测度和勒贝格-斯蒂尔杰斯测度以及相应的积分理论推广到更一般的集合上，就需要做一系列奠基工作，其中之一是建立一些特殊的集类并研究其性质。环以及半环、σ环、代数、σ代数等重要集类正是为了这一目的而引入的。

雅各布森根雅各布森根是以右(左)拟正则性为根性质的一种重要的根。设R是任意环，若R有本原理想，则环R的一切本原理想的交称为R的雅各布森根，用J(R)表示.当R无本原理想，规定J(R)=R，此时R称为J根环(雅各布森环)。雅各布森根还可以从多种角度描述：J(R)等于R的一切左本原理想的交，又等于R的最大的右拟正则理想，它包含R的一切右拟正则右理想，还等于R的最大左拟正则理想，它包含R的一切左拟正则左理想，同时，亦等于R的一切模的极大右理想的交，也等于R的一切模的极大左理想的交，又等于{x∈R|xa是右拟正则，对任意a∈R}.雅各布森根是雅各布森(Jacobson，N.)于1945年引入的。

素环素环是一类重要的环。若环R的零理想是素理想，则称R为素环。环R是素环当且仅当下列等价条件之一成立：

1.设A，B是R的理想，若AB=(0)，则A=(0)或B=(0)。

2.R中任意非零左(右)理想的左(右)零化子为零。

3.对任意x∈R，若RxR=(0)，则x=0。2

例如，整环、单环、本原环都是素环。素环与素理想有如下关系：P是R的素理想当且仅当R/P是素环。

人物简介——雅各布森美国数学家。1910年4月 10 日生于波兰华沙，1917年随家庭移居美国。1930年获亚拉巴马大学学士学位，1934年获普林斯顿大学博士学位。曾任教于布林莫尔学院、芝加哥大学、加利福尼亚大学、北卡罗来纳大学、约翰斯·霍普金斯大学，1947年起任教于耶鲁大学。1954年被选为美国全国科学院院士。1971—1973年任美国数学会主席，1970—1974年任国际数学联盟副主席。

雅各布森的贡献主要在结合环、李代数和若尔当代数等代数领域。在结合环理论方面，他在1945年发展了环的一般结构理论并给出了该理论的一些重要应用，其中包括给出了环的根基及相应半群单纯性概念的一般定义;用本原环对半单纯环作了部分分析;本原环的结构理论和特殊情况下代数的代数理论的特定化。在李代数方面，他的贡献主要在结构理论，特别是特征为“0”的任意域上单李代数的分类，并开创了素特征李代数的结构理论。1937—1938年，他引入了p李代数的概念，并发展了不可分域扩张的伽罗瓦理论。1950年以后，他主要研究若尔当代数理论，其主要成果在表示理论并发展了类似于阿廷结合环结构理论的结构理论。雅各布森著有《环论》(Theory of Rings，1943)、《抽象代数讲义》(Lectures in Abstract Algebra，3 vols， 1951—1964)、《环的结构》(Structure of Rings， 1956;1964年修订本)、《李代数》(Lie Algebras，1962)、《若尔当代数的结构与表示》(Structureand Representations of Jordan Algebras，1968)、《例外李代数》(Exceptional Lie Algebras，31971)、《PI代数》(PI-Algebras，1975)等书。教科书《代数基础》(Basic Algebra)被广为采用，有中译本。