[科普中国]-法曲率

法曲率是刻画曲面在某一方向的弯曲程度的量，其有一定的计算公式。曲线 C 的曲率和曲面 S 沿 C 的切方向的法曲率具有联系。

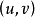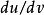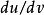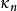定义曲面的第二基本型和第一基本型之比是依赖曲面的点 和在该点的切方向 的函数，称为曲面在该点沿切方向 的法曲率 ，即

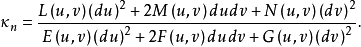
性质直观上，在曲面上经点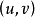、与切方向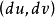相切段曲线段曲率向量在曲面的单位法向量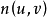上的投影恰好是法曲率。

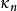实际上，设曲面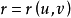上的曲线 C 的参数方程是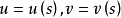，则

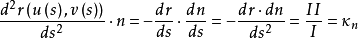它依赖曲线 C 的切方向，而与 C 的具体形状无关。

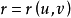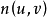特别是，用经过点、由和切方向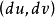所张点平面与曲面相交得到的曲线（称为法截线）作为平面曲线在该点的相对曲率就是曲面在该点沿切方向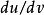的法曲率。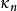

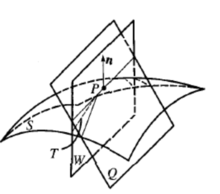
设 C 是曲面 S 上的一条曲线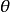， 是曲线 C 的主法向量和曲面的法向量的夹角，则曲线 C 的曲率和曲面 S 沿 C 的切方向的法曲率的关系： 。

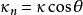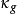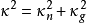另外，如果曲线 C 在曲面 S 上的测地曲率是 ，则有 。1

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学