定义定义一
设 为任意一个环,如果
为任意一个环,如果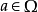 且有自然数n使
且有自然数n使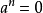 ,则说
,则说 是
是 的一个诣零元素,又当n是使
的一个诣零元素,又当n是使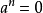 的最小自然数时,就说n是
的最小自然数时,就说n是 的诣零指数,设L是
的诣零指数,设L是 的一个左理想,如果L中元素都是诣零元素,则说L是
的一个左理想,如果L中元素都是诣零元素,则说L是 的一个诣零左理想;如果有自然数n使
的一个诣零左理想;如果有自然数n使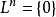 ,则说L是
,则说L是 的一个幂零左理想。同理可定义诣零右理想与想诣零两边理以及幂零右理想与幂零两边理想。显然,幂零左(右、两边)理想为特殊的诣零左(右、两边)理想,还可以定义诣零环、诣零子环、幂零环、幂零子环等,显然理想的诣零性与幂零性均为环同态下的不变性。2
的一个幂零左理想。同理可定义诣零右理想与想诣零两边理以及幂零右理想与幂零两边理想。显然,幂零左(右、两边)理想为特殊的诣零左(右、两边)理想,还可以定义诣零环、诣零子环、幂零环、幂零子环等,显然理想的诣零性与幂零性均为环同态下的不变性。2
定义二若A是环R的理想,则一般仅有关系式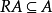 和
和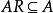 ,如果R有单位元,则必有RA=AR=A,所以我们常把R称为单位理想,称理想A为幂等理想,如果
,如果R有单位元,则必有RA=AR=A,所以我们常把R称为单位理想,称理想A为幂等理想,如果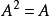 ,因而必有
,因而必有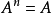 ,
,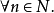 称理想A为幂零理想,如果存在自然数n使
称理想A为幂零理想,如果存在自然数n使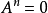 (注意:未必有
(注意:未必有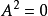 ),易见,此时A中任意n个元素的乘积必为0,特别,A中任意元都是幂零元,任意元都是幂零元的理想称为诣零理想。因此,幂零理想必是诣零理****想,反之不然,例如,交换环中幂零元全体成诣零理想,但未必是幂零理想3。
),易见,此时A中任意n个元素的乘积必为0,特别,A中任意元都是幂零元,任意元都是幂零元的理想称为诣零理想。因此,幂零理想必是诣零理****想,反之不然,例如,交换环中幂零元全体成诣零理想,但未必是幂零理想3。
相关性质与定理命题1  的两个幂零左理想
的两个幂零左理想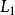 与
与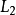 之和
之和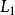 +
+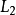 仍为幂零的。
仍为幂零的。
命题2 如果L是 的一个幂零左理想,则
的一个幂零左理想,则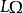 为
为 的幂零两边理想。
的幂零两边理想。
命题3
⑴如果L是 的幂零左理想,则
的幂零左理想,则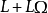 为
为 的幂零两边理想。
的幂零两边理想。
由定义易知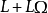 为
为 的两边理想(它是
的两边理想(它是 的含L的最小两边理想),其幂零性可由命题1、2而知。此命题说明
的含L的最小两边理想),其幂零性可由命题1、2而知。此命题说明 的幂零左理想恒可扩大成为
的幂零左理想恒可扩大成为 的幂零两边理想。
的幂零两边理想。
⑵如果R是 的幂零右理想,则
的幂零右理想,则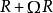 为
为 的幂零两边理想。
的幂零两边理想。
命题4 任意环 的一切幂零左、右及两边理想的并集N是
的一切幂零左、右及两边理想的并集N是 的一个诣零两边理想。
的一个诣零两边理想。
命题5  的两个诣零两边理想A,B之和A+B仍为诣零的。
的两个诣零两边理想A,B之和A+B仍为诣零的。
命题6  含有非0的诣零左理想等价于
含有非0的诣零左理想等价于 含有非0的诣零右理想。
含有非0的诣零右理想。
命题7 任意环 的一个子环S为诣零的必要而且只要有
的一个子环S为诣零的必要而且只要有 的诣零两边理想M使S在自然同态映射
的诣零两边理想M使S在自然同态映射
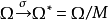
下的映象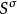 为诣零的。
为诣零的。
命题8 如果S为 的诣零子环,M为
的诣零子环,M为 的诣零两边理想。则
的诣零两边理想。则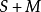 (即所有
(即所有 作成的子集,
作成的子集,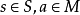 )为
)为 的诣零子环。
的诣零子环。
对于幂零性同样有:
命题9  的子环S为幂零的
的子环S为幂零的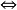 有
有 的幂零两边理想M使S在(
的幂零两边理想M使S在(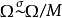 )下的映象
)下的映象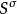 为幂零的。
为幂零的。
命题10 如果S与M分别是 的幂零子环与幂零两边理想,则
的幂零子环与幂零两边理想,则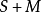 为
为 的幂零子环。
的幂零子环。
定理1  的上指数为n的左(右)理想(
的上指数为n的左(右)理想(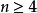 )恒含有
)恒含有 的上指数为3或2的左(右)理想。
的上指数为3或2的左(右)理想。
定理2  的上指数为3的左理想L必含有
的上指数为3的左理想L必含有 的上指数为2的左理想。
的上指数为2的左理想。
定理3  中上指数为2的左理想L恒为
中上指数为2的左理想L恒为 的若干个幂零指数为2的幂零左理想的并集。1
的若干个幂零指数为2的幂零左理想的并集。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国