我们所接触到的空间,大至宇宙,小至细胞,其中都充满着五光十色、变幻纷杂的曲线。诸如太阳系行星的轨道,飞机的航道,盘山蜿蜒的公路,沙发里的弹簧,织物图案花纹,齿轮和凸轮的轮廓,生命遗传物质DNA的双螺旋结构,等等。
在人们接触到的曲线中,最简单的要算是直线和圆了。这些曲线是初等平面几何中讨论的对象。其次较为复杂的曲线是二次曲线,即椭圆、双曲线和抛物线。这些已经在平面解析几何里学习过,讨论的方法是用坐标和一元二次代数方程。
对于更复杂的曲线,仅仅用初等代数一般是不能解决问题的。研究更加一般的光滑曲线的几何性质,微积分则是有力的工具。我们可以用微积分来推导三个刻划一条空间曲线几何性质的基本几何量,就是弧长、曲率和挠率。1
空间曲线的表示式参数方程一条空间曲线的表示式是
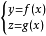
或
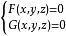 每一组方程都是把一条空间曲线作为两个曲面的交线,用上述表示式研究空间曲线会引起形式不对称和计算繁琐的缺点。为了避免这些缺点,我们经常采用参数方程:
每一组方程都是把一条空间曲线作为两个曲面的交线,用上述表示式研究空间曲线会引起形式不对称和计算繁琐的缺点。为了避免这些缺点,我们经常采用参数方程:
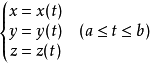 表示一条空间曲线,其中
表示一条空间曲线,其中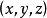 表示曲线上一点在右手系直角坐标系下的坐标,
表示曲线上一点在右手系直角坐标系下的坐标,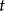 为参数。
为参数。
如果把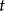 看成时间,那么该曲线可以看成是空间质点从时刻
看成时间,那么该曲线可以看成是空间质点从时刻 到
到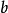 之间的运动轨迹。不过一般而言,
之间的运动轨迹。不过一般而言,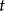 不具备这个物理意义,而且参数的选择并不是唯一的。例如对于参数变换
不具备这个物理意义,而且参数的选择并不是唯一的。例如对于参数变换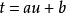 ,参数方程的各函数将改变形式而曲线本身形状并不改变。1
,参数方程的各函数将改变形式而曲线本身形状并不改变。1
向量方程设右手直角坐标系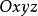 中的坐标基向量为
中的坐标基向量为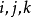 ,我们可以将曲线的参数方程写成向量方程:
,我们可以将曲线的参数方程写成向量方程:
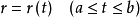 式中
式中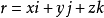 代表曲线上点的位置向量。
代表曲线上点的位置向量。
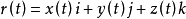 称为关于变量
称为关于变量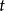 的向量函数,常简写成分量表示
的向量函数,常简写成分量表示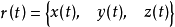 。
。
空间曲线的三个元素弧长设一空间曲线决定于参数方程
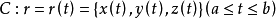 式中各函数有直至三阶的连续导数,即
式中各函数有直至三阶的连续导数,即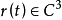 。
。
设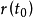 是曲线
是曲线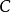 上的任意点,简称
上的任意点,简称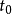 点。
点。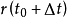 是其邻点。这两点决定一个向量,即:
是其邻点。这两点决定一个向量,即:
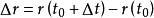 除以
除以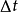 便得到方向相同而长度不同的向量。当
便得到方向相同而长度不同的向量。当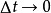 时,从曲线
时,从曲线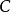 的连续性可知
的连续性可知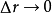 ,而且
,而且
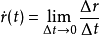 是曲线
是曲线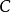 在
在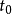 点的一个切向量。
点的一个切向量。
当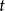 变动时,曲线
变动时,曲线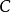 可以看成质点
可以看成质点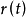 的轨迹,
的轨迹,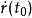 的物理意义就是质点在
的物理意义就是质点在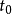 点的速度向量,
点的速度向量,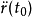 则是加速度向量。
则是加速度向量。
设曲线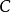 的两邻点
的两邻点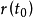 和
和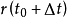 之间的弧长为
之间的弧长为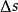 ,对应的弦长为
,对应的弦长为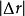 ,有
,有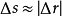 ,从而得到
,从而得到
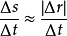
当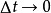 时,便可得到
时,便可得到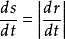 ,对该式从
,对该式从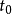 到
到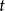 积分得到
积分得到
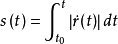
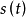 称为曲线
称为曲线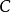 从
从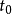 到
到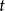 的弧长,上式也可用分量形式表示为
的弧长,上式也可用分量形式表示为
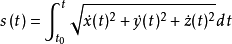
曲率对于一条空间曲线,采用自然参数 表示的方程
表示的方程
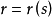 其一阶导数
其一阶导数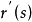 表示曲线的单位切向量,我们进一步考虑它的二阶导数
表示曲线的单位切向量,我们进一步考虑它的二阶导数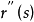 ,给出如下定义:
,给出如下定义:
空间曲线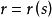 在点
在点 的曲率为
的曲率为
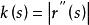 当
当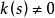 时,其倒数
时,其倒数
 称为曲线在点
称为曲线在点 的曲率半径。1
的曲率半径。1
挠率曲线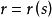 关于其弧长
关于其弧长 的一阶导数
的一阶导数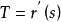 是单位切向量,但是二阶导数
是单位切向量,但是二阶导数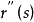 一般并不是单位向量函
一般并不是单位向量函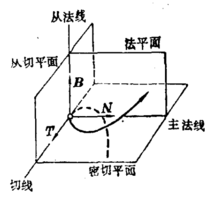 数,因为其长度即曲线在该点的曲率
数,因为其长度即曲线在该点的曲率 一般不等于1,但是二阶导数垂直
一般不等于1,但是二阶导数垂直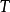 ,当
,当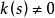 时,我们把
时,我们把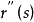 规范化为单位向量,即
规范化为单位向量,即
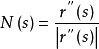 称为曲线在点
称为曲线在点 的主法向量,而且称
的主法向量,而且称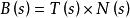 为曲线在同一点的从法向量。
为曲线在同一点的从法向量。
由于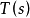 垂直
垂直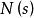 ,且
,且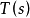 和
和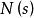 都是单位向量,从而
都是单位向量,从而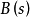 是垂直于
是垂直于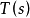 和
和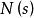 的单位向量。由此我们在曲线上任意点获得一组两两正交的单位向量组
的单位向量。由此我们在曲线上任意点获得一组两两正交的单位向量组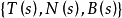 。这样与曲线紧密联系的三个向量形成了一个单位正交标架。
。这样与曲线紧密联系的三个向量形成了一个单位正交标架。
不落在同一平面上的空间曲线,我们称之为挠曲线。如同弯曲的概念一样,曲线论中也有“挠扭”的概念,用于描述一条曲线在一点偏离密切平面的程度。为了描述这种偏离度,我们将用到密切平面的变化率,也就是密切平面的法向量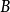 的变化率,这样就导出曲线的“挠率”这一概念。
的变化率,这样就导出曲线的“挠率”这一概念。
定义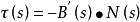 称为曲线在点
称为曲线在点 处的挠率。显然平面曲线的挠率恒为零。1
处的挠率。显然平面曲线的挠率恒为零。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国