[科普中国]-通用覆盖群

概念介绍

通用覆盖群是指相关于给定李群的一种李群。设G和G1为连通李群。若存在G1到G上之同态映射f，使任取g∈G，f(g)为G中离散子集；且任取g1∈f(g)，存在g1在G1中之邻域U1以及g在G中之邻域U，使得f：U1→U为到上之同胚，则G1称为G的覆盖群，f称为G1到G上之覆盖映射。记(G，f)为G之覆盖群，若J1及J分别为G1及G之李代数，则f的微分df为J1到J上之李代数同构。设G为连通李群，(G1，f1)，(G2，f2)为G的覆盖群。若存在连通李群G1到G2上的同构σ，可得交换图(右图)，即f2°σ=f1，则称(G1，f1)和(G2，f2)是等价的。互相等价的覆盖群的性质完全相同。若给定连通李群G，则在等价意义下惟一存在一个覆盖群(G^，f^)，使得G^为连通且单连通李群，此时称(G^，f^)为G的通用覆盖群。因此，若任意给定李代数L，则在群之同构意义下惟一存在一个连通且单连通李群G^，使得G^之李代数和给定的李代数L同构，且任一连通李群G，只要G的李代数和L同构，则必存在G^到G上之覆盖映射f^，使得(G^，f^)为G之通用覆盖群，这时同态核f^(e)=Γ^为G^之离散正规子群，所以包含在G^之中心C(G^)中，且连通李群G和商群G^/Γ^同构，Γ^称为连通李群G之庞加莱(Poincaré，(J.-)H.)群，也就是G的一阶同伦群。

群群是一种只有一个运算的、比较简单的代数结构；是可用来建立许多其他代数系统的一种基本结构。

设G为一个非空集合，a、b、c为它的任意元素。如果对G所定义的一种代数运算“·”(称为“乘法”，运算结果称为“乘积”)满足：2

(1)封闭性，a·b∈G;

(2)结合律，即(a·b)c = a·(b·c);

(3)对G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，则称G对于所定义的运算“·”构成一个群。例如，所有不等于零的实数，关于通常的乘法构成一个群;时针转动(关于模12加法)，构成一个群。

满足交换律的群，称为交换群。

群是数学最重要的概念之一，已渗透到现代数学的所有分支及其他学科中。凡是涉及对称，就存在群。例如，可以用研究图形在变换群下保持不变的性质，来定义各种几何学，即利用变换群对几何学进行分类。可以说，不了解群，就不可能理解现代数学。

1770年，拉格朗日在讨论代数方程根之间的置换时，首先引入群的概念，而它的名称，是伽罗华在1830年首先提出的。3

李群李群是由挪威数学家S.李创立的一类连续变换群。

1870年前后，S.李开始研究连续变换群的概念，并用它们阐明微分方程的解，将微分方程进行分类。1874年，他建立了李群的一般理论。一个李群可以表示成如下形式：

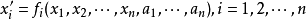其中fi对xi和ai都是解析的，xi是变量，而ai是参数，(x1，x2，…，xn)表示n维空间中的一点。变量或参数都取实数值或复数值。1883年，S.李借助于一组微分方程定义连续变换群。他的目的是用各种不同的方法把常微分方程的不同类型化成可由积分求解的形式，并建立起它们之间的一致性。S.李证明，如果一阶常微分方程接受由某个无穷小变换所确定的变换群，那么这个微分方程的解就可由积分式表达。他还考察了许多种带有已给变换的方程。这样一来，S.李就依据无穷小变换把微分方程进行分类。

李群理论在最初的相当长一段时间内仅与一些微分方程的积分有联系，而与数学的其他分支关系不大。在19世纪的最后10年以及20世纪，李群理论在各种不同方向，主要是代数学和拓扑学方面得到了迅速的发展，成为数学的一个重要分支。李群理论的第一个近代化的叙述是由原苏联数学家庞特里亚金于1938年给出的。20世纪50年代，李群理论的发展进入了一个新的阶段，主要标志是代数群论的创立。代数几何方法的应用使李群理论的经典结果得到新的阐述，从而揭示了它与函数论、数论等理论的深刻联系。紧接着，p进李群的理论也得到重大发展。事实上，李群理论与数学的几个主要分支都有联系：通过李变换群与几何学、拓扑学的联系，通过线性表示论与分析的联系等。李群在物理学和力学中也有着重要应用。4

连通无向图G中，若点u，v之间存在路，则称u，v是连通的.若无向图G的任意二点都是连通的，则G称为连通图。

若认为无向图G的任意点“自身是连通的，则无向图G中点的连通关系是点集的一个等价关系，即适合自反性、对称性、传递性的关系。于是，G的点集V能划分成互不相交的子集V1，V2，…，Vk的并；V1∪V2∪…∪Vk=V，i≠j，Vi∩Vj=φ。不同的Vi，Vj，中的点互不连通，而同一Vi中的点彼此连通。每个Vi的点及它们关联的边构成G的子图Gi，称为G的一个连通分支；W (G) =k称为G的连通分支数，当W (G)=1时，称G是连通图。

无向连通图的这两个定义是等价的。

对于有向图G来说，若存在u到v的有向路，则说u可达v。当然，u可达v时，未必u可达v。有向图G的任意二点都相互可达时，G称为强连通的；若G的任意二点，至少有一点可达另一点，则G称为单侧连通的；若G略去边的方向时是连通图； 则弥G是弱连通的。强连通图必是单侧连通图；单侧连通图必是弱连通图。其逆均不真。

覆盖群覆盖群又叫拟单群，是较单群更广的一类群。设G是有限群，若G等于它的导出群，并且G/Z(G)为单群，则称G为拟单群。若G为拟单群，则常称G为G/Z(G)的覆盖群。有限群G的次正规拟单子群H称为G的分支或分量。5