[科普中国]-有理性定理

有理性定理是有关高维射影簇双有理分类的一个定理。

定义设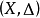 是正常的川又对数终极配对，且 是有效的，使得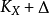 不是数值有效的。

设有整数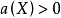 使得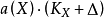 是卡吉耶除子，H 是数值有效的全息除子，定义

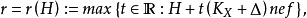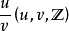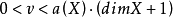则 r 是有理数，形如 ，且 。1

全息除子【big divisor】

对紧 n 维代数簇 X 上卡吉耶除子 D ，如果存在常数 c>0 ，使得当k》1时，有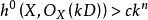，则称 D 为全息除子。

“全息”在这里的含义是指该除子能传递簇的所有双有理不变性质，相较“大”在意思上更贴切。

卡吉耶除子卡吉耶除子是指环空间(X,?X)上除子的芽层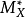/?*X的一个整体截面。这里MX表示X上亚纯（或有理）函数的芽层，即使得每个开子集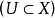对应环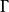(U,?X）的全分式环的层，而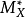和?*X则分别是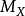和?X里可逆元的层。一个卡吉耶除子可被一族局部方程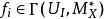所确定，其中{ Ui} 是X的开覆盖，函数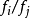则是层?*X在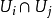上的截面。一个卡吉耶除子如果是自然映射(M*X/?*X)的像，则称为主除子。两个卡吉耶除子称为是线性等价的，如果二者相差一个主除子。使得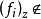?*Xx的x∈M的集合称为除子的支集（support of the divisor ）。卡吉耶除子类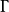(M*X/?*X)关于线性等价的商群记为CaCI(X)。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学