[科普中国]-希尔伯特模曲面

希尔伯特模曲面是模形式的 2 维推广。设O是一个判别式为 d 的实二次域的代数整数环，希尔伯特模群作用于 2 维的上半复平面，可以通过添加有限多个点使正规复空间紧致化，从而得到一个正规曲面。

简介希尔伯特模曲面是模形式的 2 维推广。设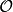 是一个判别式为 d 的实二次域的代数整数环。

希尔伯特模群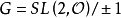 作用在两个单位圆盘的乘积 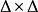上，通过添加有限多个点使正规复空间 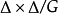紧化，从而得到一个正规曲面。通过一典范方法解消曲面上的奇点，从而得到光滑紧复曲面 Y(d) ，称 Y(d) 为具有判别式 d 的希尔伯特模曲面。

性质Y(d) 是单连通的，所以有 q=(Y(X))=0。

当 d=5，8，12，13，17，21，24，28，33，60时，Y(d) 是有理曲面；

当 d=29，37，40，41，44，56，57，69，105 时，Y(d) 双有理等价 K3 曲面；

当 d=53，61，65，73，76，77，85，88，92，93，120，140，165 时，Y(d) 是椭圆曲面。

其他情形的 Y(d) 是一般型极小曲面。1

相关概念有理曲面在代数几何里，有理曲面（rational surface）是指一个双有理等价于投影平面的曲面；换句话说，即为一个二维有理簇。有理曲面是复曲面的十余种恩里克斯-小平分类中最简单的一类，且是第一个被研究的曲面。

K3曲面以库默尔，凯勒，小平邦彦命名的曲面，这是具有平凡典范丛的单连通紧复解析曲面，其小平维数是 0 。其满足 Pg=1，q=0，K≡0。

椭圆曲面椭圆曲面就是以椭圆曲线 (亏格的Riemann面) 为一般纤维，具有这种纤维结构的复曲面 (2维紧复流形)。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学