切层是代数簇上的点的切空间构成的层。更精确地说,对于代数簇 X,切层就是 X 上一次微分所构成的层的对偶层。
定义切层是代数簇上的点的切空间构成的层。
更精确地说,对于代数簇 X,切层就是 X 上一次微分所构成的层 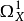 的对偶层,即?x= ℋ om(
的对偶层,即?x= ℋ om(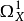 ,Ox)。
,Ox)。
当 X 为光滑代数簇时,切层是一个局部自由层,其秩等于 X 的维数。1
法层(normal sheaf)
法层是代数簇 X 的闭子概形 Y 上的一个层。
若 Y 在 X 中的理想层为 ?,则称 ?/?2 为 Y 在 X 中的余法层,它的对偶层NY/X=ℋ om(?/?2,OY)称为 Y 在 X 中的法层。
当 X 和 Y 都是光滑代数簇时,法层 NY/X 是一个局部自由层,其秩等于 Y 在 X 内的余维数 r 。这时有一个典范的正合列0→?Y→?X⊗OY→NY/X→0 。
切空间切空间是在某一点所有的切向量组成的线性空间。
切空间是微分流形在一点处所联系的向量空间,欧氏空间中光滑曲线的切线、光滑曲面的切平面的推广。
微分流形M在p∈M处的全体切向量的集合记为TpM,对于Xp,Yp∈TpM,α∈R与f∈C∞(p),设:

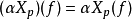
因而TpM是实数域R上的n维向量空间,称为微分流形M在p处的切空间。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国