 在同调代数中,内射对象与投射对象是内射模与投射模在阿贝尔范畴中的推广,二者的定义相对偶。以下固定一个阿贝尔范畴。
在同调代数中,内射对象与投射对象是内射模与投射模在阿贝尔范畴中的推广,二者的定义相对偶。以下固定一个阿贝尔范畴。
若对象 使得函子
使得函子 为正合函子,则称
为正合函子,则称 为投射对象。
为投射对象。
若对象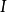 使得函子
使得函子 为正合函子,则称
为正合函子,则称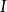 为内射对象。
为内射对象。
若对每个对象 都存在投射对象
都存在投射对象 及满射,则称
及满射,则称 有充足投射元。若对每个对象
有充足投射元。若对每个对象 都存在内射对象
都存在内射对象 及单射
及单射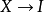 ,则称
,则称 有充足内射元。对于有充足投射元(或内射元)的阿贝尔范畴,可以考虑对象的投射分解(或内射分解)。1
有充足内射元。对于有充足投射元(或内射元)的阿贝尔范畴,可以考虑对象的投射分解(或内射分解)。1
同调代数是数学的一个分支,它研究同调与上同调技术的一般框架。同调代数是一门相对年轻的学科,其源头可追溯到代数拓扑(单纯形同调)与抽象代数(合冲模)在十九世纪末的发展,这两门理论各自由庞加莱与希尔伯特开创。
同调代数的发展与范畴论的出现密不可分。大致说来,同调代数是(上)同调函子及其代数结构的研究。“同调”与“上同调”是一对对偶的概念,它们满足的范畴论性质相反(即:箭头反向)。数学很大一部分的内在构造可藉链复形理解,其性质则以同调与上同调的面貌展现,同调代数能萃取这些链复形蕴含的资讯,并表之为拓扑空间、层、群、环、李代数与C*-代数等等“具体”对象的(上)同调不变量。谱序列是计算这些量的有力工具。
同调代数肇始即在代数拓扑中扮演要角。其影响日渐扩大,目前已遍及交换代数、代数几何、代数数论、表示理论、算子代数、偏微分方程与非交换几何。K-理论是一门独立的学科,它也采用同调代数的办法。2
阿贝尔范畴在数学中,阿贝尔范畴(或称交换范畴)是一个能对态射与对象取和,而且核与上核存在且满足一定性质的范畴;最基本的例子是阿贝尔群构成的范畴Ab。阿贝尔范畴是同调代数的基本框架。
一个范畴 若满足下述条件,则称阿贝尔范畴:
若满足下述条件,则称阿贝尔范畴: 是加法范畴,所有态射皆有核与上核,所有态射皆为严格态射。只满足前两个条件者称作预阿贝尔范畴。
是加法范畴,所有态射皆有核与上核,所有态射皆为严格态射。只满足前两个条件者称作预阿贝尔范畴。
若取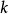 为一交换环,则在上述定义中以k-加法范畴代换加法范畴,便得到k-阿贝尔范畴之定义。3
为一交换环,则在上述定义中以k-加法范畴代换加法范畴,便得到k-阿贝尔范畴之定义。3
在范畴论中,正合函子(或译作恰当函子)是保存有限极限的函子。在阿贝尔范畴中,这就相当于保存正合序列的函子。
设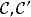 为阿贝尔范畴,
为阿贝尔范畴, 为加法函子。若对每个正合序列
为加法函子。若对每个正合序列
 取
取 后得到的序列
后得到的序列
 仍为正合序列,则称
仍为正合序列,则称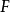 为正合函子
为正合函子 。
。
由于正合序列总能拆解为短正合序列,在定义中仅须考虑短正合序列即可。
此外,若对每个短正合序列 ,其像截去尾端零对象后
,其像截去尾端零对象后 为正合序列,则称
为正合序列,则称 是左正合函子;类似地,若
是左正合函子;类似地,若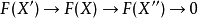 为正合序列,则称
为正合序列,则称 是右正合函子。正合性等价于左正合性+右正合性。3
是右正合函子。正合性等价于左正合性+右正合性。3




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国