全子范畴(full subcategory)是一种特殊的子范畴,设D为C的子范畴,若子范畴定义中的条件HomD(A,B)⊆HomC(A,B)改为HomD(A,B)=HomC(A,B),则称D为C的全子范畴。阿贝尔群范畴是群范畴的全子范畴,交换环范畴是环范畴的全子范畴,但存在不是全子范畴的子范畴。例如,令范畴Φ的对象为一切Sn=(0,1,2,…,n),n=0,1,…,态射Sn→Sm,n≤m定义为Sn的各分量变成Sm中大于或等于此分量的分量,态射合成按常规合成定义,若限制其中的态射满足f(0)=0,则得到Φ的一个子范畴Φ1,但Φ1不是Φ的全子范畴1。
基本介绍范畴D称为C的子范畴(sub category),如果 是
是 的子类,且
的子类,且 ,而且D中的态射的合成和C是一样的。例如,Poset是Set的子范畴。又如果
,而且D中的态射的合成和C是一样的。例如,Poset是Set的子范畴。又如果 ,有
,有 ,则称D是C的全****子范畴(full subcategory)。例如,Grp是Mon的全子范畴。
,则称D是C的全****子范畴(full subcategory)。例如,Grp是Mon的全子范畴。
相关概念模范畴对偶性模范畴对偶性(duality in categories of modules)是模范畴等价的对偶概念。设C和D是两个范畴, 和
和 是两个逆变函子,若有自然等价
是两个逆变函子,若有自然等价 和
和 ,则称
,则称 与
与 是对偶函子,而称C与D是对偶范畴。模论中考虑较多的问题是:在模范畴
是对偶函子,而称C与D是对偶范畴。模论中考虑较多的问题是:在模范畴 和
和 中是否有全子范畴
中是否有全子范畴 和
和 ,以及
,以及 和
和 之间的加性逆变函子
之间的加性逆变函子 ,使得
,使得 与
与 是对偶函子,
是对偶函子, 和
和 是对偶范畴,此性质就称为模范畴的对偶性1。
是对偶范畴,此性质就称为模范畴的对偶性1。
模范畴等价模范畴等价(equivalence of categories of modules)是对模范畴的一种刻画,存在等价函子的模范畴称为等价的模范畴。设 是模范畴,若存在加性共变函子
是模范畴,若存在加性共变函子
 和
和
 使得GF自然同构于
使得GF自然同构于 的恒等函子,FG自然同构于
的恒等函子,FG自然同构于 的恒等函子,则称函子F与G等价,且称模范畴
的恒等函子,则称函子F与G等价,且称模范畴 与
与 是等价的,记为
是等价的,记为
 此时,也称环A与B是森田纪一相似的,记为
此时,也称环A与B是森田纪一相似的,记为 。两个模范畴C,D等价的充分必要条件是,存在全忠实函子
。两个模范畴C,D等价的充分必要条件是,存在全忠实函子 ,并且对任意
,并且对任意 ,总有
,总有 ,使得
,使得 同构于
同构于 。模范畴的等价理论是模论的一个重要组成部分,森田纪一(Morita Kiiti)于1958年讨论了两个模范畴的等价和对偶,得到了一系列深刻而又漂亮的结果,森田纪一的工作是经典的阿廷-韦德伯恩定理在模上的推广,现在他的工作已发展成所谓的森田纪一理论。
。模范畴的等价理论是模论的一个重要组成部分,森田纪一(Morita Kiiti)于1958年讨论了两个模范畴的等价和对偶,得到了一系列深刻而又漂亮的结果,森田纪一的工作是经典的阿廷-韦德伯恩定理在模上的推广,现在他的工作已发展成所谓的森田纪一理论。
森田纪一对偶定理森田纪一对偶定理(Morita theorem on duality)是模范畴对偶性的重要定理。设C和D是 和
和 的全子范畴,且
的全子范畴,且 ,又对任意
,又对任意 ,若
,若 ,则必有
,则必有 ,这里
,这里 。若
。若 和
和 是对偶函子,则一定存在双模
是对偶函子,则一定存在双模 ,使得:
,使得:
1.
2.
3. C和D中每个模都是U自反模。
在一个模范畴中,不可能每一个模都是U自反模,所以模范畴的对偶只能在全子范畴之间存在1。
塞尔子范畴塞尔子范畴(Serre subcategory)是阿贝尔范畴的一种子范畴,它在同调代数等学科中有重要应用,也是定义商范畴的基础概念。设C为阿贝尔范畴,D为C的全子范畴且满足:对C中任意的正合列 ,
, 当且仅当
当且仅当 且
且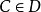 (即,
(即, 当且仅当B的子对象与商对象都是D的对象),此时称D为C的塞尔子范畴,塞尔子范畴仍为阿贝尔范畴1。
当且仅当B的子对象与商对象都是D的对象),此时称D为C的塞尔子范畴,塞尔子范畴仍为阿贝尔范畴1。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国