[科普中国]-希尔伯特模形式

概念

希尔伯特模形式(Hilbert modular form)是一种模形式概念的推广。设K是全实有限次代数数域，K之共轭为K(1)，K(2)，…，K(n)，n=[K∶Q]，α∈K的共轭表为α(1)，α(2) ，…，α(n)。若D为K的主整环，ΓD=SL(2，D)，定义ΓD在：1

Hn={Z=(z1，z2，…，zn)|zi∈H}

上的作用为：

其中：

则ΓD是SL(2，R)n的不可约离散子群，称为(狭义)希尔伯特模群。定义在H上关于希尔伯特模群的自守形式就称为希尔伯特模形式，注意这里自守因子为：

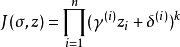
当n=1时就是普通的模形式。关于希尔伯特模形式也有类似于模形式、西格尔模形式等情形的结果。

模形式论一种特殊的自守形式的理论。由（J.-）H.庞加莱所发展的一般的富克斯群上的自守形式，是属于单复变函数论的一个课题。由E.赫克所创的模形式是对于模群Sl2(Z)或其他算术群的自守形式，就其内容和方法而言，则应为数论的一部分。它在以后的发展中与椭圆曲线理论、代数几何、表示论等有十分深刻的联系而成为数学中的一个综合性学科。

模形式是指满足以下两个条件的函数ƒ(z)：①ƒ(z)是上半平上的全纯函数，在∞处的傅里叶展开式为α0+α1q+α2q2+…,式中q=e2πiz,αi是常数；②若则式中Г 表示所有行列式等于1的二阶整数方阵构成的群,称之为模群；k是某个整数，称之为模形式ƒ(z)的权。因而，ƒ(z)又称为群Г上权为k的模形式。 上半平面h上的变换 称为模变换。

全体模形式构成的线性空间记为Mk(Г)，它是复数域上的一个有限维向量空间。若以dk表示它的维数，则当k1时,定义函式中求和号┡表示对不等于(0,0)的所有整数组(m,n)求和。等号右端的无穷级数是绝对收敛的，所以Gk(z)在h上是全纯函数。且可证明Gk(z)属于M2k(Г)。Gk(z)称为艾森斯坦级数，它在∞处的傅里叶展开式为 又一个重要的例子是权为12的模形式 它与G妇(z)和G娬(z)同属于M12(Г),因为d12=2，所以在墹(z)、G妇(z)和G娬(z)之间一定存在一个线性关系,实际上有墹(z)=(60G2(z))3－27(140G3(z))2，进而可证明Mk(Г)是由适合4α+6b=k的诸G屶(z)(z)在复数域上张成的，这里α、b为非负整数。

令 这些τ(n)都是整数。1916年，S.A.拉马努金关于τ(n)的性质提出如下的猜想：当m与n互素时,τ(mn)=τ(m)τ(n);当p为素数,α为正整数时1920年，L.J.莫德尔证实了这一猜想。赫克在Mk(Г)中引入了一类线性算子（赫克算子），类似于τ(n)所具有的性质正是这类算子的公共本征矢的傅里叶系数所具有的性质。这些公共本征矢组成了Mk(Г)的一组基。拉马努金关于τ(n)的另一个猜想1974年P.德利涅证实了这一猜想。

当模形式ƒ(z) 的傅里叶展开式中常数项α0为零时，ƒ(z)称为歧点型模形式。

由墹(z)的乘积表达式可知墹(z)≠0(z∈h)。因此定义函数它是一个权为零的模形式。在所有模变换之下不变的亚纯函数称为 Г上的模函数。可见j(z)是模函数，进而可证明Г上任意模函数都可表成j(z)的有理式。

对于Г 的子群，也可类似地定义模形式。常见的这类子群有 式中N为正整数。研究这些群上的模形式空间的构造,是模形式论的一个重要课题。

模形式论还可用于把一个整数表成几个整数的平方和的问题。以r_s(n)表示把n表成s个整数平方和的所有不同的表法个数，显然有

这是二次剩余符号,εd对所有奇数d有定义,当d呏1（mod4）时，εd=1，当d呏3(mod4)时，εd=i，平方根(сz+d)1/2的幅角总取在之内。设k为正奇数,在模形式的定义中，用j(r，z)k代替条件②中的(сz+d)k，即为权是半整数k/2的模形式定义，例如θ3(z)是Г0(4)上权为3/2的模形式。2

模一个重要的代数系统。它是一个带算子区A的交换(加)群M。给定集合A与交换群M，若定义了a∈A与x∈M的乘积ax∈M，并且这个积满足条件：

1.a(x+y)=ax+ay (a∈A，x，y∈M)，

则称A为M的算子区，称M为带算子区A的模，又称为A上的模或A模。这时，由对应(a，x)→ax确定的映射A×M→M，称为A作用到M上的运算。任意a∈A可诱导出M的自同态aM：x→ax，而考虑交换群M能否成为A模就是看能否给出映射：

μ： A→End(M)， a→aM.

特别地，考虑A是结合环，若满足上述条件1的A模还满足：

2.(a+b)x=ax+bx;

3.(ab)x=a(bx);

即映射μ：A→End(M)为环同态，则称M为左A模或左环模。由于A到M上的运算是写在左侧，所以M就称为左A模，记为AM。类似地，有右A模M，记为MA。若A有单位元1，且又满足条件：

4.1x=x (x∈M);

则称M为酉模或幺模。

人物简介——希尔伯特德国数学家。出生于普鲁士的哥尼斯堡。1882—1885年在哥尼斯堡大学学习。在学期间，受到著名数学家雅可比、维尔斯特拉斯、费·纽曼、韦伯等人的指导，大大激发了数学兴趣和才能。他的两上好友A·胡尔威茨和闵可夫斯基对他数学方面的成长也产生过巨大的影响。 1885年，他因不变式理论方面的论文获博士学位。 1892年任母校的数学副教授。1895年由F·克莱因的提议担任了哥廷根大学的教授。哥廷根大学是具有优秀数学传统的学府，高斯、黎曼等人曾在这里工作。希尔伯特在这里团结了一大批当代的著名数学家和物理学家，使哥廷根成了20世纪前期世界数学的中心与理论物理学家聚会的场所。他逝世的前一年被柏林科学院授予荣誉院士的称号。希尔伯特不愧是本世纪领头的数学家。他的数学兴趣十分广泛，并且所到之处都留下了光辉足迹。早期研究不变式理论。采用直接的、非算法的方法证明了果尔丹证明的代数不变式整基有限完备系的存在定理，对后来的抽象代数的发展起了推动作用。重新整理了欧几里得几何的公理体系，于1899年发表了 《几何基础》一书，把欧几里得几何整理为从公理出发的纯粹演绎系统，并把注意力转移到公理系统的逻辑结构，成为近代公理化思想的代表作。他提出的狄里克莱原理以及对积分方程、变分法、华林问题的研究，在数学史上都很有意义。晚年致力于数学基础问题，把公理系统的无矛盾性看成数学可靠性的标准，是数学基础中形式主义学派的代表人物。1990年他在巴黎国际数学家代表会上的讲演中提出23个数学问题，概括了19世纪数学发展中暴露的主要问题，后来称为希尔伯特问题。对西方的数学研究有较大的影响。希尔伯特为后人留下的著作有《数论报告》、《线性积分方程一般理论基础》、《几何基础》，以及其他论文3卷，还有与别人合写的 《数理逻辑基础》、《数学物理方法》、《直观几何学》、《数学基础》。3