简介
设X是拓扑空间,M包含于X,h是从x到X的同胚。易证,如果x是M的内点,则h(x)仍为h(M)的内点,如果x是M的边界点,则h(x)仍为h(M)的边界点。但是,如果h只在M上定义,则边界点或内点未必是不变的。例如,设X是E3空间中由平面(x1,x2,0)及x3轴组成,M是X中由x3轴组成的子集。h是一从x3轴到x1轴的同胚映射,则点(0,0,1)是M的一个内点,但它的象h(0,0,1)不再是h(M)的内点,因为,在X中不存在包含点h(0,0,1)而完全含于h(M)的开集。然而,对于欧氏空间来说,不会发生这种情形,内点的同胚象必仍为内点,边界点的同胚象必仍为边界点。这个定理,就是区域不变性定理。1
区域不变性定理的简化证明定义欧氏空间En的方体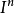 为
为
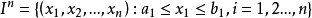
则下列两引理成立
引理A对于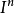 的内点x,不论点x的邻域V(x)如何小,存在从
的内点x,不论点x的邻域V(x)如何小,存在从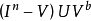 到
到 的连续映射:
的连续映射:
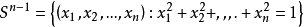
不能连续地扩张到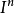 。
。
引理B对于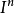 的边界点x,存在点x的小邻域V(x),不论从
的边界点x,存在点x的小邻域V(x),不论从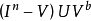 到
到 的连续映射如何,均能连续地扩张到
的连续映射如何,均能连续地扩张到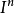 。
。
为了证明引理A,用反证法。假设相反,x是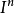 的内点,取闭包含于二
的内点,取闭包含于二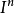 的球邻域为V(x),取f为以x为投影中心从
的球邻域为V(x),取f为以x为投影中心从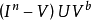 到
到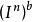 (与
(与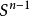 同胚)的中心投射。显然,f使
同胚)的中心投射。显然,f使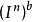 的点不动。如果存在f的连续扩张
的点不动。如果存在f的连续扩张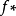 ,则
,则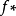 仍使
仍使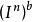 的点不动。
的点不动。
考虑连续映射F,:
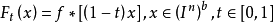
则常值映射F1(x)与恒等映射Fo(x)同伦,然而这是不可能的。下面我们来证明常值映射F1(x)与恒等映射Fo(x)不能同伦。为了方便起见,假设Ft是定义在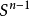 球面之上的。
球面之上的。
设 是欧氏空间En的两个点,则En的所有满足下列条件的点
是欧氏空间En的两个点,则En的所有满足下列条件的点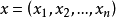 :
:
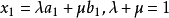
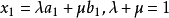
的集合记为(a,b),称为以a,b为端点的线段。欧氏空间En的子集合M称为凸的,当且仅当a∈M,b∈M蕴涵(a,b)cM。
为了证明引理B,设x是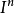 的任一个边界点,取以x为中心不完全包含
的任一个边界点,取以x为中心不完全包含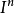 的球邻域V。设f是从
的球邻域V。设f是从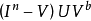 到
到 的任一个连续映射。由于x是边界点,必存在一属于V而不属于
的任一个连续映射。由于x是边界点,必存在一属于V而不属于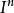 的点q,以q为中心将
的点q,以q为中心将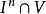 向Vb投射,以二记此中心投影,显然二是连续映射。考虑连续映射F:
向Vb投射,以二记此中心投影,显然二是连续映射。考虑连续映射F:
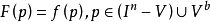
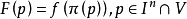
于是F(P)是一从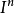 到
到 的连续映射,而且F是f的连续扩张。
的连续映射,而且F是f的连续扩张。
由于x是M的内点,故必存在一以x为内点完全含于M中的小方体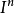 。如果h(x)不是11(M)的内点,则h(x)更不是h(
。如果h(x)不是11(M)的内点,则h(x)更不是h(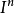 )的内点,因而是h(
)的内点,因而是h(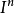 )的边界点。由引理B,存在h(x)的开邻域V,满足引理B的条件。又因h为同胚映射,故对于h(x)的开邻域V,存在x的开邻域Wc
)的边界点。由引理B,存在h(x)的开邻域V,满足引理B的条件。又因h为同胚映射,故对于h(x)的开邻域V,存在x的开邻域Wc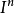 ,使
,使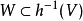 。由引理A,存在从
。由引理A,存在从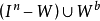 到
到 的连续映射f,不能连续扩张到
的连续映射f,不能连续扩张到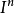 。然而,另一方面,将引理B运用于h(
。然而,另一方面,将引理B运用于h(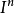 )的边界点h(x)及开邻域V,考虑连续映射fh-1,对于
)的边界点h(x)及开邻域V,考虑连续映射fh-1,对于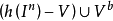 的任一点y,
的任一点y,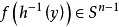 。可知fh-1能连续地扩张到h(r),因此,f也能连续地扩张到
。可知fh-1能连续地扩张到h(r),因此,f也能连续地扩张到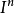 。得出矛盾。所以,h(x)不能是h(M)的边界点。证完。2
。得出矛盾。所以,h(x)不能是h(M)的边界点。证完。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国