[科普中国]-有向系统

有向系统(directed system)是特殊的有向偏序集。若一个偏序集的任意两个元素有上界，则称此偏序集为有向偏序集。

概念有向系统(directed system)是特殊的有向偏序集。若一个偏序集的任意两个元素有上界，则称此偏序集为有向偏序集。设P(A)表示A的幂集，B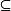P(A)，并且B≠∅。若〈B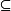，〉是一个有向偏序集，则称B是一个有向系统，其中〈B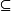，〉表示B关于集合包含关系构成的偏序集。1

偏序集偏序集是特定的集。它是一类主要的序关系集。具体地说，集合E连同其上的偏序R构成的关系集(E，R)，一般记为P=(E，≤)。所谓偏序(或序关系)是一类具有自反性、反对称性和传递性的二元关系。例如，数之间的不大于关系，自然数之间的整除关系，集合之间的包容关系等。把集合E的基数称为偏序集P的阶。阶为有限值的偏序集称为有限偏序集。而在P上，对于任意元素x，y，区间[x，y]均为有限偏序集时，称P为局部有限偏序集。这两类偏序集是组合理论中的主要研究对象。偏序集上所有链的长度的最小上界，或上确界，称为偏序集的长度，记为l(P)。偏序集中最大反链包含的元素数目，称为偏序集的宽度，记w(p)。对于以下图为哈塞图的偏序集P，有l(P)=3，w(P)=2。偏序集的子关系集仍为偏序集，而且必有全序集作为其子关系集。

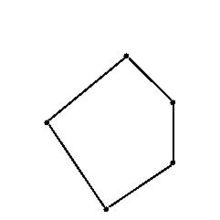
全序集全序集亦称线性序集。又称链.一类重要的偏序集。若偏序集P适合公理P4：若对任意x，y∈P，x