舒尔指数(Schur index)是指与有限中心单代数相似的可除代数的次数。对域F上有限维中心单代数A,从同构意义上来说存在惟一中心可除代数D和某自然数n,使得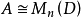 。将相应于A的可除代数D的次数
。将相应于A的可除代数D的次数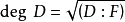 称为A的舒尔指数,记为
称为A的舒尔指数,记为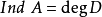 。舒尔指数也可对任意可分代数定义,特别地,有限维半单代数
。舒尔指数也可对任意可分代数定义,特别地,有限维半单代数 ,若对每个单代数
,若对每个单代数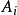 的舒尔指数定义为
的舒尔指数定义为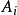 作为它中心上代数的舒尔指数
作为它中心上代数的舒尔指数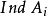 ,则
,则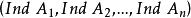 就称为A的舒尔指数1。
就称为A的舒尔指数1。
设 为
为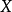 在
在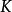 上的舒尔指数,并记为
上的舒尔指数,并记为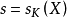 。
。
定理1设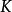 的有限域,则总有
的有限域,则总有 ,换句话说对应于指标
,换句话说对应于指标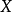 的绝对不可约表示总可以在
的绝对不可约表示总可以在 上实现。
上实现。
定理2 设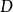 为
为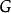 的一个绝对不可约表示,其指标为
的一个绝对不可约表示,其指标为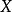 。
。
a) 若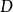 可以在
可以在 的某扩域
的某扩域 上实现,并且
上实现,并且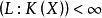 ,则舒尔指数
,则舒尔指数 是
是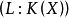 的因子。
的因子。
b) 存在 的一个扩域
的一个扩域 ,使
,使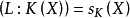 ,而且
,而且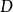 可在
可在 上实现。
上实现。
c) 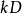 在
在 上可实现当且仅当
上可实现当且仅当 是k的因子。
是k的因子。
d)  是
是 的因子。
的因子。
定理3设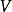 为不可约
为不可约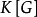 -模,
-模, 为
为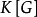 的分裂域而
的分裂域而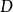 为
为 在
在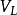 上的表示
上的表示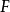 的绝对不可约分量,那么,
的绝对不可约分量,那么,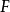 是完全可约的,它的绝对不可约分量就是全体在K与D共轭的表示
是完全可约的,它的绝对不可约分量就是全体在K与D共轭的表示 ,而且每一个等价类都以相同的重数s出现,若
,而且每一个等价类都以相同的重数s出现,若 为D的指标,则s等于
为D的指标,则s等于 在
在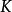 上的舒尔指数
上的舒尔指数 ,若
,若 为
为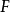 的指标,则
的指标,则
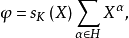 其中
其中 取遍
取遍 在K上的伽罗华群
在K上的伽罗华群 的元素。
的元素。
定理4设 ,而
,而 为
为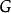 在
在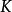 的某扩域
的某扩域 上的绝对不可约指标。
上的绝对不可约指标。
a) 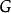 恰有一个在
恰有一个在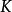 上的不可约指标
上的不可约指标 ,使
,使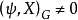 ,这里
,这里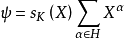 ,此处H为
,此处H为 在
在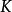 上的伽罗华群。
上的伽罗华群。
b) 若 为
为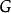 在
在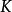 上的指标,则
上的指标,则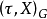 总能被舒尔指数整除2。
总能被舒尔指数整除2。
舒尔(Schur,Issai,1875.1.10-1941.1.10)是德国数学家。生于俄国莫吉廖夫,卒于巴勒斯坦特拉维夫(现属以色列)。曾在柏林大学读过书。1911年执教于波恩,1919年任柏林大学数学教授。1935年受纳粹当局迫害离职,1939年移居巴勒斯坦。舒尔是当时德国最优秀的犹太数学家之一,他追随其师弗罗贝尼乌斯研究群的表示理论,以发现“舒尔函数”和证明“舒尔定理”而著称。他第一个通过线性函数变换来研究所谓“表示”,并首先在代数数域问题上使用了“舒尔指数”,还重建了群的特征理论(1905年)。此外,他对群论、矩阵理论、代数方程论、数论、级数理论、积分方程和函数论等领域均有论述。舒尔的研究工作对现代数学的发展有很大影响。1973年,德国著名的施普林格出版社出版了他的论文集。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国