[科普中国]-惯性群

惯性群

惯性群是分解群的一个正规子群。它所决定的商群同构于相应的剩余域的伽罗瓦群。若N是域F的一个正规扩张，C与π分别为N的一个赋值环与对应的位，并且N-，F-分别是赋值环C，C∩F的剩余域，则N-是F-的正规扩张，且有一个从分解群G(C，F)到伽罗瓦群Aut(N-/F-)的满同态φ，使得对：2

当且仅当：

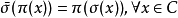同态φ的核称为C关于F的惯性群，记为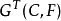。惯性群可如下给出：

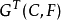其中MC是C的赋值理想。惯性群在N中的固定子域称为C关于F的惯性域。

群群是一种只有一个运算的、比较简单的代数结构；是可用来建立许多其他代数系统的一种基本结构。

设G为一个非空集合，a、b、c为它的任意元素。如果对G所定义的一种代数运算“·”(称为“乘法”，运算结果称为“乘积”)满足：

(1)封闭性，a·b∈G;

(2)结合律，即(a·b)c = a·(b·c);

(3)对G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，则称G对于所定义的运算“·”构成一个群。例如，所有不等于零的实数，关于通常的乘法构成一个群;时针转动(关于模12加法)，构成一个群。

满足交换律的群，称为交换群。

群是数学最重要的概念之一，已渗透到现代数学的所有分支及其他学科中。凡是涉及对称，就存在群。例如，可以用研究图形在变换群下保持不变的性质，来定义各种几何学，即利用变换群对几何学进行分类。可以说，不了解群，就不可能理解现代数学。

1770年，拉格朗日在讨论代数方程根之间的置换时，首先引入群的概念，而它的名称，是伽罗华在1830年首先提出的。

子群子群是群的特殊的非空子集。群G的非空子集H，若对G的乘法也成为群，则称H为G的子群，记为H≤G。若子群H≠G，则称H为G的真子群，记为HG或简记为H