简介

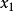 设线性无关的向量组
设线性无关的向量组
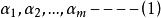
可由向量组
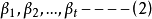
线性表示,则m簇t,并且可从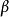 中选出t一m个向量,使得向量组
中选出t一m个向量,使得向量组
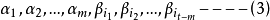
与向量组(2)等价。
上述定理通常称为替换定理。
证明方法一设向量组(2)的极大无关组为

显然r≤t,由于(1)可由(2)线性表示,故(4)也是
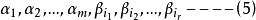
的一个极大无关组,又因
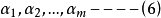
线性无关,故m≤r,又r≤t,从而m≤t。
因(5)的秩为r,显然m≤r,适当选择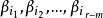 可把(1)扩充为(5)的一个极大无关组。
可把(1)扩充为(5)的一个极大无关组。
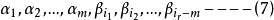
由于(4),(7)均为(5)的极大无关组,故(4)与(7)等价,故(7)是(2)的极大无关组,从(2)中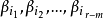
之外选取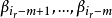 ,可得向量组
,可得向量组
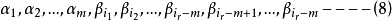
显然,(8)和(2)等价。
方法二由题设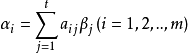 ,得
,得
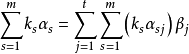
若m>t,则
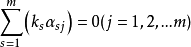
必有非零解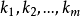 ,(未知量个数大于方程个数,故也)。从而有
,(未知量个数大于方程个数,故也)。从而有 ,即
,即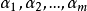 线性相关,这与题设矛盾,因此m≤t。
线性相关,这与题设矛盾,因此m≤t。
下证第二部分,设向量组(2)的秩为r,不防设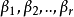 是(2)的极大无关组,则
是(2)的极大无关组,则
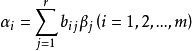
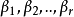 由上述证明可知必有m≤t,由于
由上述证明可知必有m≤t,由于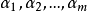 线性无关,故由(4)中
线性无关,故由(4)中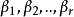 的系数组成的矩阵
的系数组成的矩阵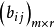 的秩必为m,故它一定存在一个m阶子式不为0,不防设它的前m列构成的m阶子式不为0,由此易知
的秩必为m,故它一定存在一个m阶子式不为0,不防设它的前m列构成的m阶子式不为0,由此易知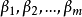 可由
可由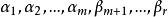 线性表示,故
线性表示,故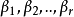 与
与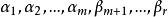 等价,又因为是(2)的极大无关组,因此
等价,又因为是(2)的极大无关组,因此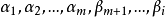 与
与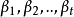 等价。12
等价。12




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国